By Francisco Aranda
Polarization-maintaining fibers rely on asymmetry to produce birefringence, preventing mixing of polarization states and the resultant polarization-mode dispersion.
In many telecommunications applications, it is important to maintain control over the polarization of light transmitted through an optical fiber. Such control is complicated by the fact that a standard axially symmetric single-mode optical fiber actually transmits two orthogonally polarized modes. In an ideal world, this would be no problem: for perfectly round fiber, the two orthogonal modes are degenerate, meaning that no difference exists between their propagation constants. Furthermore, if the fiber is perfectly straight, no coupling exists between these modes; hence no transfer of energy takes place between them. Should one of these modes be launched at the input of such a fiber, the same mode would appear at the end of the fiber.
In the physical world, optical fibers are neither free of ambient effects nor perfectly axisymmetric and completely straight. As a result of environmental influences, the polarization state of the propagated light in an optical fiber is subject to fluctuations produced by changes in ambient conditions such as stress, heat, bending, and so on (this is the basis for the use of optical fibers as sensors). In addition, even when a fiber is designed to have axial symmetry, slight elliptical deformations arise during fabrication. This residual ellipticity separates the propagation constants of the orthogonal modes and causes signal-degrading polarization-mode dispersion (PMD). The magnitude of PMD can be reduced by improvement of the fiber's physical circularity, equalization of thermal expansion coefficients of core and cladding, and preform spinning during draw.
Differing notations can be used. The two orthogonal degenerate modes in an axially symmetric single-mode fiber can be termed HE11x and HE11y, with their principal electric field components lying along the x and y directions respectively. Alternatively, the two modes can be represented as clockwise and counterclockwise circularly polarized HE11 modes. A more common notation used to represent the modeswhich abandons specific mention of the electric and magnetic fieldsis the linearly polarized (LP) notation. In this notation, HE11 becomes LP01 (see Fig. 1).
Polarization control
In many important fiberoptic applications, a polarization-state control scheme is required. The complete solution to these problems rests in the use of polarization-maintaining (PM) fiber. For PM fiber, PMD is quite large if both modes are launched, but can be reduced to zero by launching light along one of the principal axes of the fiber, thus launching only one mode. In this case, polarization-mode dispersion increases linearly with length and is expressed in units of time over distance. In one example, PMD for a PM fiber might reach 1 ns/km when both modes are launched.
For regular single-mode fiber, coupling between the two orthogonal modes induced by random fluctuations of the birefringence along the fiber length tends to equalize the propagation times of the modes. In this case, PMD scales with the square root of length and is on the order of 0.1 ps/km0.5.
FIGURE 2. Schematic of four types of PM fiber illustrates their cross-sectional geometry. Outlined shapes portray regions of differing glass type. Polarization-maintaining and absorption-reducing (PANDA), oval inner clad, and bowtie fibers generate birefringence through residual stress produced when the fiber is fabricated. The birefringence in oval-core fiber is produced by the shape of the core itself.
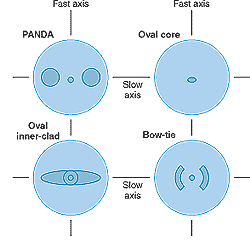
In the broadest of senses, PM fibers can be divided into low-birefringence and high-birefringence fibers.1 When focusing on high-birefringence fibers that are available commercially, it is noted that such high-birefringence fibers can be further subdivided into those whose birefringence is induced via a geometrical effect and those whose birefringence is induced via a residual stress effect. The most-common types of commercially available PM fibers are bowtie, polarization-maintaining and absorption-reducing (PANDA), oval inner cladding, and oval core (see Fig. 2). The first three are examples of residual-stress-induced birefringence, while the oval core is an example of geometrically induced birefringence.
More parameters
In addition to the usual single-mode-fiber parameters such as mode-field diameter, cutoff wavelength, and so on, there are other relevant parameters to consider when using PM fibers. For example, the core of a PM fiber has two distinct values of refractive index; thus, light traveling through it has two different propagation velocities, one for each orthogonal mode. The higher the modal birefringence, the more rapidly the two polarization modes will become decoupled and polarization preserved.
Modal birefringence, a dimensionless quantity, is simply the difference in the two refractive indices. Both geometrical and material anisotropies contribute to the modal birefringence of a PM fiber. Geometrical contributions arise from asymmetries in the structures surrounding the core, as well as from deviations from circularity of the core itself. Material contributions arise from the residual thermal stresses present at the core of the fiber; they may exist even when the core is perfectly circular such that no geometrical effects exist. The largest values of modal birefringence are observed for fibers possessing large material birefringence.
Beat length is important because it measures how well a fiber maintains polarization. It is a measure of how fast the two orthogonal modes become decoupled and thus cease to exchange energy. Beat length is equal to the wavelength of the transmitted light divided by the modal birefringence. Fibers with short beat lengths preserve polarization more strongly than those with long beat length. For a bowtie type of fiber, typical beat lengths are a few millimeters, whereas for regular single-mode fiber it is on the order of tens of meters.
The so-called H-parameter for a given length of fiber is a commonly used measure of the polarization-maintaining properties of that piece of fiber, and is intimately related to the measured extinction ratio. It can be approximated as the product of the inverse of the length of the piece of fiber under consideration times the ratio of unwanted to wanted light measured at the end of the fiber piece; here, "wanted" refers to the amount of light in the mode that was initially launched. Special care must be taken when measuring and reporting the value of the H-parameter, given that its value is dependent on such factors as the environmental conditions and winding conditions under which the fiber is measured.
Attenuation is the amount of light lost at the relevant wavelength per unit length; its units are decibels per kilometer. Care must be exercised when dealing with high-birefringence fibers because the attenuation for the two orthogonal modes may be significantly different.
Uses for polarization maintaining fiber
Polarization-maintaining fibers can be found in many telecommunications and sensor applications. These include high-performance transmission laser pigtails, polarization-based modulators (for example, lithium niobate), high-data-rate communications systems, polarization-sensitive components, polarization-maintaining couplers (fixed and variable ratio), polarization splitters, coherent telecommunications systems, gyroscopes, high-voltage current sensors, and optical-networking components.
In the majority of sensor applications, the fiber lengths used are shorton the order of hundreds of meters. As a result, the fibers used in sensors can have greater losses than those used in telecommunications applications. Tolerance to greater losses allows the fiber manufacturer more flexibility in the use of compound glasses and the use of glasses whose composition is not based on silica.
Glass compositions with high Verdet constant (a measure of polarization rotation caused by the interaction of a magnetic field with the glass) become the sensing material for high-voltage current sensors used in the utility and power-distribution industry. For other uses, glass compositions can be formulated to desensitize the fiber to undesired effects such as temperature variations. Polarization-maintaining fiber has also found widespread acceptance in the aerospace industry as the preferred type of fiber for use in fiberoptic gyroscopes.
REFERENCE
1. J. Noda, K. Okamoto and Y. Sasaki, J. Lightwave Technol. LT-4 (8), 1071 (1986).
FRANCISCO ARANDA is senior product manager of optical components at StockerYale, 32 Hampshire Rd., Salem, NH 03079; e-mail: [email protected]