New dispersion-compensation technology is evolving to meet the demands of higher-performance fiberoptic systems. The first generation of dispersion compensation remains the standard approach for chromatic dispersion. Components with fixed chromatic dispersion are added to the system to offset the fixed chromatic dispersion of the transmission line, reducing the cumulative dispersion. With careful design, that approach greatly enhances transmission distances at speeds up to 10 Gbit/s. Yet the success of static compensation remains limited by how well the fixed dispersion of the compensating fiber or other components offsets that of the transmission line.
The next logical steps are compensating components with dispersion that can be tuned in magnitude and wavelength, and adjusted dynamically. Tunability and dynamic compensation don't have to go together. Dynamic compensation requires a feedback loop that measures dispersion and then sends control signals to adjust the dispersion in the compensator. Tuning, however, can be done without a dynamic feedback loop, either as a manual adjustment by an on-site technician or as an operation remotely controlled from an operations center.
The requirements depend on the application. Dynamic compensation is a must for polarization-mode dispersion, which varies randomly and rapidly with time depending on environmental conditions, causing bursts of noise. Chromatic dispersion does not have the same rapid fluctuations, although it does change with temperature. For a 2000-km link, the drift with 10∞C to 20°C of temperature change can reach 50 ps/nm, the maximum limit for 40-Gbit/s systems, but these changes are not rapid.
Principles of compensation
FIGURE 1. Static compensation of chromatic dispersion leaves slight differences in total dispersion across a range of wavelengths, so the range of cumulative dispersion spreads with distance.
The workhorse of static chromatic dispersion has been dispersion-compensating fiber, which has negative chromatic dispersion several times larger than the positive chromatic dispersion of single-mode transmission fiber. Adding a length of dispersion-compensating fiber offsets the transmission fiber's dispersion, giving low overall dispersion. Dispersion slope also must be balanced for wavelength-division multiplexing. The balancing is not perfect because the slopes don't match exactly, so the cumulative dispersion through the system varies with wavelength (see Fig. 1).
Such dispersion plots are helpful in visualizing the impact of chromatic dispersion, but many dispersion-compensation techniques can be better understood by viewing chromatic dispersion as a phase shift between wavelengths in the signal. The phase shift is uniform through a segment of compensating fiber, which offers only static compensation. Changing the phase shift makes it possible to tune or dynamically change the amount of compensation.
A variety of approaches can produce the desired phase shifts. Some produce periodic peaks in phase shift as a function of wavelength or frequency. Matching the peaks to the optical channels in standard DWDM frequency grids makes it possible to tune dispersion simultaneously on many separate channels. Other techniques are limited to working at one specific wavelength.
Fiber Bragg gratings
One of the best-developed tuning techniques is based on changing the properties of fiber Bragg gratings developed earlier for static dispersion compensation. The phase shift in fiber-grating compensators depends on a chirp applied to the spacing of high-index layers in the grating. If the spacing increases along the length of the fiber grating, the longer wavelengths travel farther through the grating before being reflected. This delays the longer wavelengths relative to the shorter ones. If the distance between long- and short-wavelength parts of the grating is 1 mm, the longer wavelengths are delayed by about 10 ps.
The phase shift caused by the grating can be tuned by changing the distance between the high-index zones in the grating, the refractive index of the glass, or both. Doing one or both changes the point in the fiber at which particular wavelengths are reflected. Either heating the fiber or applying mechanical stress along its length can produce the required changes.
There is an additional complication—changes that are linear along the length of the grating don't provide the differential phase shift needed to adjust chromatic dispersion. The change must be nonlinear along the length of the fiber. The required nonlinearity can be achieved either by starting with nonlinear spacing of the fiber grating itself, or by applying a stress nonlinearly. Mechanical stress normally is uniform along the length of a fiber, but it is possible to vary the temperature nonlinearly along the fiber grating for temperature tuning.
An inherent limitation of fiber gratings is that their tunability covers only a limited wavelength range. The current range is one to eight DWDM optical channels. Single-channel tuning gives better granularity in adjustment, but it greatly increases the component count and expense.
All-pass filters and etalons
Phase shifting also is possible in an "all wave" filter, which ideally transmits all light at all wavelengths in its operating range, but can phase shift some wavelengths. Two important examples are etalons and ring resonator cavities.
In the familiar Fabry-Perot etalon, light passes through a cavity consisting of two partly transparent mirrors. Light can resonate inside the cavity if the round-trip distance (D) between the two mirrors is an integral number of wavelengths l in a medium with refractive index n, or 2D = Nl/n. These resonant wavelengths are delayed within the cavity, causing a phase shift relative to other wavelengths. However, a Fabry-Perot etalon is not a true all-pass filter because light can exit from either of the two mirrors.
A less-familiar type of etalon, the Gires-Tournois design, does function as an all-pass filter because the rear mirror is totally reflective, so all light exits through the partly transparent front mirror (see Fig. 2). As in a Fabry-Perot etalon, resonances occur where the round-trip distance equals an integral number of wavelengths, and light at these resonances experiences a phase delay, spending more time in the cavity than wavelengths away from the resonator. Unlike the Fabry-Perot etalon, the Gires-Tournis etalon reflects all input light from the front surface, acting as an all-pass filter.
FIGURE 3. Phase delay in a Gires-Tournois etalon varies periodically. For WDM systems, the peaks are spaced to match standard optical channels. Tuning moves the phase delay curve relative to the channels varying phase delay similarly across a number of channels.
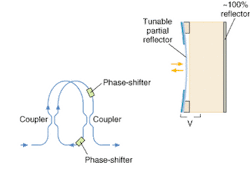
Changing the spacing between the mirrors can tune these resonances and the resulting phase delay. One approach moves a flexible front mirror back and forth relative to the total reflector. Alternatives include temperature tuning of the refractive index, which has the same effect of shifting the resonant wavelengths. The resonances are not infinitely sharp, but are spread over a range of wavelengths (see Fig. 3). We normally think of a change in the cavity length as changing the resonant wavelength. However, in a WDM system the channel wavelength is fixed, so we see instead a change in the phase delay at the channel wavelength. The etalon structure has multiple resonances at regularly spaced wavelengths, which can be matched to channel wavelengths, so phase-delay tuning can be applied over many channels, although the technique cannot tune the dispersion slope.
Another type of all-pass filter with tunable phase delay is the ring resonator shown in Fig. 2. The ring includes a pair of thermo-optic phase shifters, which are adjusted to tune the phase delay, and thus tune the chromatic dispersion. (With a single phase shifter, the ring gives a fixed phase delay.) This approach is not as well developed as the etalon all-pass filter, but can be made in integrated-optic form, offering the potential of low cost manufacture.
Other tuning
Chromatic dispersion can be tuned in several other ways. Among the most important is the virtual phase array, in which input light enters an etalon at an angle inclined to the normal. Light bounces along the length of the etalon between the mirrors, with some emerging from the output mirror at each bounce. These separate beams interfere as if they were coming from an array waveguide or the grooves of a diffraction grating, causing phase delays that can be tuned by tuning the optics.
Virtual phased arrays have been built from bulk optics. The same principles have been used in an integrated optic tunable compensator with a pair of fixed arrays separated by a thermo-optic lens that can be tuned to change the chromatic dispersion.
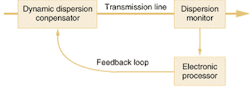
All these optical techniques can, in principle, come in two versions. A simple tunable dispersion-compensation system is adjusted to meet the requirements of the transmission system, then left in this static setting until the system is changed in some way. Alternatively, they can be operated dynamically, with a monitoring system sensing chromatic dispersion, and a feedback system dynamically using this measurement to adjust the compensator (see Fig. 4).
FIGURE 4. Dynamic dispersion compensation is based on a feedback loop. A monitor measures dispersion, generating a signal that is fed to control electronics, which generate a signal that adjusts the compensating electronics to reduce dispersion. The same principles apply for chromatic and polarization dispersion, and whether compensation is for single channels or multiple channels.
A key practical issue is whether the compensator is tuned for a single optical channel, or whether it operates over a range of closely spaced channels. Single-channel systems can provide the most precise compensation, but are more costly.
Development trends
Dynamic compensation is a must for polarization-mode dispersion because of its inherent variation with time. In this case, PMD measurements are fed back through a control circuit to polarization-adjusting optics, in a system similar to that shown in Fig. 4. The principles are the same as for dynamic compensation of chromatic dispersion, but the time response must be faster.
Polarization-mode dispersion compensation was a hot topic during the telecom bubble because it is required for long-distance transmission at 40 Gbit/s. Promising technologies were developed, but in the post-bubble world most have been put on the shelf to concentrate on near-term markets. The slump in installation of new systems also has slowed development of tunable chromatic-dispersion compensators.
Yet development has not stopped, and research continues on new compensation technologies. Planners expect to need them in the future, but—as in many other development areas—the future has been a bit delayed as companies deal with near-term issues.