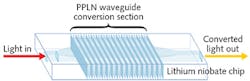
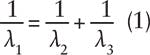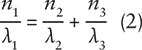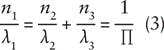Nonlinear Optics: PPLN waveguides perform quantum frequency conversion

Second-order nonlinear optical (NLO) interactions are sometimes referred to as "three-wave mixing," since they involve interactions among three optical waves of wavelengths λ₁, λ₂, and λ₃.³ To conserve energy, these three wavelengths must satisfy the relation (by convention taking λ₁ to be the shortest wavelength):

where n₁, n₂, and n₃ are the refractive indices at the respective wavelengths. In a bulk device, the birefringence of the crystal is often used to satisfy Eq. 2 by proper selection of the propagation direction(s) relative to the crystal axes. That is not generally an option in a waveguide device, so instead the technique of quasi-phase matching (QPM) is used.

where П is the period, or pitch, of the structure.

If two of the wavelengths are specified, the third is determined by Eq. 1. The necessary poling period to realize that frequency conversion process is then determined by Eq. 3. Note that accurate determination of П requires accurate knowledge of the dispersion relation of the material. For bulk devices, the indices can be determined from published temperature- and wavelength-dependent Sellmeier equations, but in waveguide devices the effective indices must be determined through detailed modeling.

PPLN waveguides

In bulk NLO devices, the efficiency is limited by divergence of the beam, with most of the conversion occurring near the beam waist where the intensity is highest. Optical waveguides are used to maintain high incremental conversion efficiency throughout the length of the device.

In lithium niobate (LiNbO₃), most waveguides are fabricated by diffusion of dopants—either titanium or zinc ions or protons in most cases—to a depth of a few micrometers. The refractive index increases with dopant concentration, so that the diffused region forms the waveguide core. Proton-exchanged or zinc-diffused waveguides are preferred for high-power applications, since they are less susceptible to optical damage from photorefractive effects.

In proton exchange, protons are substituted for lithium ions in the LiNbO₃ lattice. After the initial proton-exchange step, an annealing step at 300°–350°C is carried out to diffuse the protons and restore the NLO coefficient in the near-surface region. The result is an annealed proton-exchange (APE) waveguide.

APE waveguides have an asymmetric mode profile and relatively high dispersion, since the peak index occurs at the LiNbO₃-air interface. A more symmetrical, buried index profile can be achieved by an additional step called reverse proton exchange (RPE). In RPE, the APE waveguide is immersed in a lithium-rich salt solution, allowing lithium ions to displace some of the previously introduced protons near the surface. The result is an index profile that peaks at a depth of 2 to 3 μm beneath the surface, producing a more symmetrical mode profile with less dispersion, better overlap among the shorter- and longer-wavelength waves, and higher input/output coupling efficiency to single-mode optical fiber.

The design concept for implementation of the non-critical phase-matched waveguide is shown in Fig. 1. Essentially, the non-critical phase-matched conversion section will consist of a widening of the waveguide to increase the confinement factor in the plane of the chip. Excitation of higher-order modes in the widened section can be suppressed by appropriate mode tapering. The propagating fundamental mode in the widened section exhibits an effective index that is determined almost entirely by the core index. This means that any fabrication-resolution-limited deviations in the diffused waveguide width will have limited impact on the bandwidth relative to a narrower waveguide.

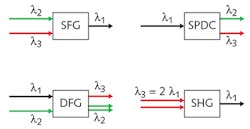
Types of three-wave interactions

Several types of three-wave interactions exist, and are classified as follows:

1. Second-harmonic generation (SHG): Input wave at λ₂ = λ₃, output wave at λ₁ = λ₂/2;

2. Sum-frequency generation (SFG): Input waves at λ₂ and λ₃, output wave at λ₁;

3. Spontaneous parametric down-conversion (SPDC): Input wave at λ₁, output waves at λ₂ and λ₃; and

4. Difference-frequency generation (DFG): Input waves at λ₁ and λ₂, output wave at λ₃. Note that for energy to be conserved, in this case there must be two output photons at λ₂ for each input photon at λ₂. For this reason, DFG is sometimes called optical parametric amplification (OPA).