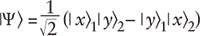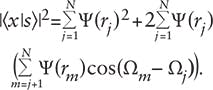Interferometry: Quantum entanglement physics secures space-to-space interferometric communications
Optical communications have been known to mankind since ancient times, beginning with the control of mirror reflections and the emission of smoke signals, extending to the use of Morse code via light signals, and culminating in today's laser communications. In all these examples, propagation through the atmosphere impacts the quality of the communications process. Therefore, terrestrial-based optical communications are somewhat limited due to atmospheric interaction with the light signals.
In a parallel track, intensive work has been devoted to protecting the secrecy of communications via the application of cryptography. The discovery of quantum entanglement via the polarization of quanta1 enabled the marriage between single-photon optical communications and cryptography in the field now known as quantum cryptography.2,3
An alternative to traditional quantum cryptography is secure interferometric communications, which is also based on quantum principles but exploits the advantages of large populations of indistinguishable photons.4 Again, atmospheric-propagation path interactions with the information-carrying quanta can cause the quantum-encoded information to decohere and be lost.
Space-to-space communications, on the other hand, where there is little or no propagation-path distortion and interaction with the carrier quanta, is an ideal application of the coupled concepts of optical communications and quantum cryptography. In this article, we indicate that both of these types of communications have a common quantum interferometric origin and that secure interferometric communications might provide a simpler, smaller, and less expensive alternative to secure satellite-to-satellite communications and to future space-vehicle to space-vehicle and space-vehicle to space-station communications. In the advent of future space-based wide-area networks, quantum-entanglement cryptography and interferometric optical communications might prove ideal for secure server-to-server and router-to-router applications.
Quantum cryptography
The concept of quantum cryptography is based on the entanglement of the polarizations of two quanta traveling in different directions and is described using the standard bra and ket formalism of the Dirac notation by the quantum probability amplitude1,5
which is widely known in its normalized version:
In the original derivation of Eq. 1, its interferometric origin was mentioned without further elaboration.5 In this regard, it should be noted that this equation has been applied to describe double-slit interference.6 Furthermore, this is the equation that has been amply applied to describe entangled states in Einstein-Podolsky-Rosen gedanken-type experiments.7,8 However, in regard to cryptography, it is often mentioned that quantum information is protected by Heisenberg's uncertainty principle.9 From a practical perspective, an important feature of this approach is that it depends on the propagation of single quanta.
Extensive work has been carried out in this area, with published highlights that indicate that cryptographic communications with single photons have been successfully carried out, in free space, over distances of 144 km.10 Typically, the experimental apparatus includes a photon-pair source, a transmission telescope, a receiving telescope, two sets of polarization-compensating optics, two beamsplitter prisms, two half-wave plates, four polarization beamsplitters, and the requisite single-photon detector.10 While single-photon detection is becoming more commonplace in the laboratory, it is still nontrivial and requires detailed expertise.11
Secure interferometric communications
Interferometric communications originate in the Dirac-based N-slit interferometric equation:4,12
So far, transmission of interferometric characters over distances of 35 m and 527 m through the atmosphere at or near sea level have been demonstrated,16,17 although this method of communication was originally conceived for outer-space communications between satellites.4
The interferometric origin of quantum entanglement
In his original 1947 to 1949 work, Ward mentions that the entanglement probability amplitude originates in the fundamentals of interference.5 Feynman also points to interference as the most fundamental of quantum principles.19 Indeed, recently it has been explicitly explained how the quantum-entanglement equation
can be derived from the Dirac interferometric principles20 that yield the generalized interferometric equation:14,21,22
Furthermore, the entanglement of n pairs of particles can be analyzed via the propagation of N pairs of channels using the Dirac interferometric principles.22 Finally, it has also been shown that Heisenberg's uncertainty principle can be outlined from interferometric principles.14,22 Thus, it is reasonable to assume that the security of quantum cryptography, via polarization entanglement, and the security of interferometric communications originate from the same foundations.
Terrestrial development
Needed for further development of secure N-slit interferometric communications is the optimization of the N-slit interferometer incorporating a miniature semiconductor laser and lightweight optics. An initial design phase using proven optical principles12,15,16 is expected to lead to the construction and testing of a prototype.
Note that the issue of beam divergence can be greatly minimized using lightweight beam-expanding optics at the transmitter stage. The generation of interferometric characters with fine spatial characteristics would obviate the need for tiled digital detectors, since interrogation of a portion of the interferogram can be used to identify the whole interferometric character.
Outer-space development
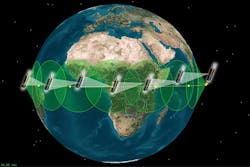
Once a lightweight prototype is developed and tested over large propagation distances, then a twin system of N-slit interferometers can be installed on two satellites. Satellite 1 will have a transmitting optics set to transmit to satellite 2 and a digital detector to receive the interferometric character from satellite 2 (see Fig. 5). In a complementary fashion, satellite 2 will have a transmitting optics set to transmit to satellite 1 and a digital detector to receive the interferometric character from satellite 1.Note that the use of large populations of indistinguishable photons should greatly simplify detection. Also, increasing the power aperture of the transmitting and receiving optical systems will enable future applications where large separation distances in space are required. The power aperture can be increased through larger telescope apertures and/or higher-power lasers.
Our calculations show that, assuming available laser technology, N-slit interferometers emitting via a slit array with a total width of ~1 m can propagate an interferogram with a total width of ~4 m at the detection plane, for an intra-interferometric distance of 2 × 106 m. This might be applicable to a network of satellites including five or six satellites per hemisphere. For space vehicles or space stations, the intra-interferometric distance D〈x∣j〉 might be increased to the 5–10 × 106 m range.
Future outlook
Once satellite-to-satellite secure interferometric communications systems are developed and tested, they would be ready for use between future space vehicles and between space vehicles and space station. More detailed experimentation, analysis, and simulation are required to prove the concept is suitable for space applications.
Due to the large distances required in any orbiting space communications network, large power apertures and rugged, sensitive photon detectors are required. Here it should be reiterated, given the excellent interplay between theory and experiment already established for interferometric communications, only detection of a portion of the interferometric character is needed rather than detection of the whole interferogram, thus significantly reducing detection requirements.
Further experimentation should enable the determination of the power-aperture requirements for a given set of mission capabilities. Once a power-aperture requirement is determined, further space-system architecture details such as size, weight, and power can be derived.
References
1. M.H.L. Pryce and J.C. Ward, Nature 160, 435 (1947).
2. A.K. Ekert, Phys. Rev. Lett. 68, 661–663 (1991).
3. C.H. Bennett, Phys. Rev. Lett. 68, 3121 (1992).
4. F.J. Duarte, Opt. Comm. 205, 313–319 (2002).
5. J. C. Ward, Some Properties of the Elementary Particles (Oxford University, 1949).
6. S. P. Walborn et al., Phys. Rev. A 65, 033818 (2002).
7. A. Einstein, B. Podolsky, and N. Rosen, Phys. Rev. 47, 777–780 (1935).
8. L. Mandel and E. Wolf, Optical Coherence and Quantum Optics (Cambridge U., 1995).
9. C.H. Bennett et al., J. Cryptology 5, 3–28 (1992).
10. R. Ursin et al., Nat. Phys. 3, 481–486 (2007).
11. A. Korneev et al., IEEE J. Sel. Top. Quantum Electron. 13, 944–951 (2007).
12. F. J. Duarte, Opt. Commun. 103, 8–14 (1993).
13. F. J. Duarte, Eur. J. Phys. 25, L57–L58 (2004).
14. F. J. Duarte, Quantum Optics for Engineers (CRC, 2013).
15. F. J. Duarte, J. Opt. A: Pure Appl. Opt. 7, 73–75 (2005).
16. F. J. Duarte, T. S. Taylor et al., J. Opt. 12, 015705 (2010).
17. F. J. Duarte, T. S. Taylor et al., J. Opt. 13, 035710 (2011).
18. F.J. Duarte, T. S. Taylor et al., J. Mod. Opt. 60, 136–140 (2013).
19. R. P. Feynman et al., The Feynman Lectures on Physics, Vol. 3 (Addison-Wesley, 1965).
20. P. A. M. Dirac, The Principles of Quantum Mechanics, 4th Ed. (Oxford University, 1978).
21. F. J. Duarte, J. Mod. Opt. 60, 1585 (2013).
22. F. J. Duarte, Tunable Laser Optics, 2nd Ed. (CRC, 2015).
About the Author
F. J. Duarte
Research Physicist, Interferometric Optics
F. J. Duarte is a research physicist at Interferometric Optics (Jonesborough, TN), an Optica Fellow (1993), and a Fellow of the Australian Institute of Physics (1987).
Travis S. Taylor
Senior Scientist, US Army Space and Missile Defense Command
Travis S. Taylor is a senior scientist at the US Army Space and Missile Defense Command (Huntsville, AL).
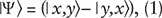
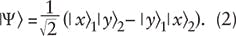
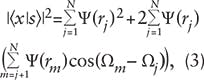
![FIGURE 1. An interferogram registered at x, for D = 35 m, λ = 632.8 nm, and N = 4 (1000 μm slits separated by 1000 μm), was recorded outside the laboratory during dusk at T ≈ 30°C. The slight asymmetry in the measured interferogram is the result of refractive-index variations of the propagation medium—in other words, slight atmospheric turbulence. N = 4 corresponds to the interferometric character c [16]. FIGURE 1. An interferogram registered at x, for D = 35 m, λ = 632.8 nm, and N = 4 (1000 μm slits separated by 1000 μm), was recorded outside the laboratory during dusk at T ≈ 30°C. The slight asymmetry in the measured interferogram is the result of refractive-index variations of the propagation medium—in other words, slight atmospheric turbulence. N = 4 corresponds to the interferometric character c [16].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/1504lfw06f1.png?auto=format,compress&fit=max&q=45?w=250&width=250)
![FIGURE 2. An intercepted and highly distorted interferogram, registered at x,D = 30 m, resulting from intra-interferometric insertion of a very thin high-surface-quality beamsplitter (10 m from the j slit array). As previously noted, the expanded laser beam (λ = 632.8 nm) interacts with N = 4, 1000 μm slits separated by 1000 μm, outside the laboratory at T ≈ 30°C [16]. FIGURE 2. An intercepted and highly distorted interferogram, registered at x,D = 30 m, resulting from intra-interferometric insertion of a very thin high-surface-quality beamsplitter (10 m from the j slit array). As previously noted, the expanded laser beam (λ = 632.8 nm) interacts with N = 4, 1000 μm slits separated by 1000 μm, outside the laboratory at T ≈ 30°C [16].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/1504lfw06f2.png?auto=format,compress&fit=max&q=45?w=250&width=250)
![FIGURE 3. The measured interferometric character b corresponding to N = 3 (570 μm slits separated by 570 μm) is shown with a diffractive pattern superimposed on the outer right wing. This superposition is accomplished by intersecting the interferogram with a transparent microscopic spider-web fiber. Here,D = 7.235 m and λ = 632.8 nm [18]. FIGURE 3. The measured interferometric character b corresponding to N = 3 (570 μm slits separated by 570 μm) is shown with a diffractive pattern superimposed on the outer right wing. This superposition is accomplished by intersecting the interferogram with a transparent microscopic spider-web fiber. Here,D = 7.235 m and λ = 632.8 nm [18].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/1504lfw06f3.png?auto=format,compress&fit=max&q=45?w=250&width=250)
![FIGURE 4. A theoretical reconstruction, via Eq. 3, is shown of the interferometric character b with the diffractive pattern superimposed on the outer right wing [18]. FIGURE 4. A theoretical reconstruction, via Eq. 3, is shown of the interferometric character b with the diffractive pattern superimposed on the outer right wing [18].](https://img.laserfocusworld.com/files/base/ebm/lfw/image/2016/01/1504lfw06f4.png?auto=format,compress&fit=max&q=45?w=250&width=250)