To exploit the carrying capacity of long-distance optical fibers, telecommunications companies are deploying wavelength-division-multiplexing (WDM) schemes and components. But even this technology will eventually become saturated with the relentless growth of communications demand, and researchers are working on the technology that is likely to replace early WDM systems. That technology is based on the phenomenon of solitons—optical pulses shaped in such a way as to resist dispersion and distortion over vast distances. Potentially, such soliton-based systems may be able to expand capacity another factor of three- to tenfold beyond conventional WDM techniques.
From canal to fiber
Solitons—or solitary waves—were first discovered by John Scott Russell in 1834, when he observed a wave propagate away from the prow of a canal barge near Edinburgh, Scotland. On horseback, he pursued the wave several miles down the canal as it ran on unchanged, not dissipating as waves generally do. It was not until 60 years later that mathematicians were able to demonstrate that such solitary waves can exist when the equations governing them are nonlinear in certain ways. In the early 1970s, researchers unraveled the underlying structure of solitons, showing that they are part of a large class of nonlinear-wave phenomena and that they have striking properties, including the ability to pass through each other unchanged.
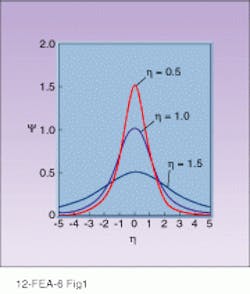
Subsequent analyses determined that solitons are governed by an equation known as the nonlinear Schroedinger equation, which is closely related to the linear Schroedinger equation that underlies all of quantum mechanics. From this equation, scientists showed that solitons had a characteristic shape that was defined mathematically by the hyperbolic secant function (see Fig. 1).
Almost immediately, in 1973, A. Hasegawa and F. Tappert at Bell Laboratories (Murray Hill, NJ) realized that solitons could be produced in optical fiber by sufficiently intense pulses of light. They also reasoned that solitons might have great applications in optical communications, because they could overcome the problem of dispersion. (In optical fibers, dispersion is an enemy of high-capacity communications. Any pulse of light is made up of a range of frequencies, and in silica, as in any other material, the index of refraction varies with frequency. As a result, the various frequencies composing a pulse travel at slightly different velocities, gradually spreading out the pulse and requiring that it be regenerated periodically by repeaters.)
In conventional systems, including those using WDM, dispersion can be minimized by tailoring the fiber material. As wavelength increases, dispersion shifts from positive to negative, going through a zero point at a given wavelength. Shifting that zero point to the 1510-nm attenuation minimum allows fibers to carry as much as 10 Gbits/s in a 1000-km span, which corresponds to a figure of merit of 10 Tbit/skm. But both attenuation and residual dispersion limits further increases in transmission bit rate per channel, and the farther the wavelengths of additional channels are from the zero-dispersion wavelength, the more dispersion they suffer.
Solitons counter this dispersion through the Kerr effect. In this effect, present in silica glass, the refractive index is increased by a small term proportional to the square of the electric field (or the power level of the radiation). For a sufficiently strong and appropriately shaped pulse, the dispersion due to chromatic factors can be exactly balanced by the Kerr effect, because the highest-frequency components of the pulse are also the highest-amplitude components. So when chromatic dispersion is negative—in silica at wavelengths longer than 1.3 µm—solitons can form and remain stable indefinitely, as long as attenuation does not reduce the strength of the pulse below a critical level.
Thus, the highest-amplitude peak of the pulse, which encounters higher nonlinear refractive index, also has the highest-frequency components, reducing the refractive index in a way that exactly balances. The net result is that every part of the soliton travels at the exact same velocity, a velocity that is directly linked to the central frequency of the soliton. Such soliton-based communications could be limited by attenuation alone.
Because the Kerr effect is relatively small in silica, it requires large radiation intensities to make a small amount of refractive-index change, but the tiny cross section of the fibers and the pulsed nature of the signal combine to make input power small. To change the index of refraction by 1% would take a radiation intensity of 3 × 1017 W/m2, the equivalent of pouring the world`s power production through one-third of a square centimeter. But to counteract the chromatic dispersion in silica requires a refractive-index change of only around 10-10, and fiber cross sections are only 10-11 m2, leading to peak power requirements of 30 mW. With a soliton pulse duration of around 10 ps and a pulse energy of 0.25 pJ, 10-Gbit/s pulse streams require laser powers of only 2.5 mW, well within the capacities of standard diode lasers.
In 1980, Linn Mollenauer and his colleagues at Bell Laboratories (Holmdel, NJ) were able to experimentally demonstrate the transmission of soliton pulses in optical-fiber loops using high-intensity laser pulses. Over the years, significant technological challenges have been overcome, so that now experimental fiber loops in the laboratory have demonstrated single-channel transmission rates of 40 Gbit/s over 6000-km loops, or 240 Tbit/skm, more than an order of magnitude better than conventional, linear transmission systems.
Fiber amplifiers make solitons practical
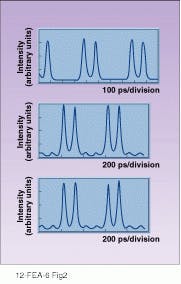
The main reason for the long lapse between the initial demonstration of solitons in 1980 and the current development is that until recently there was no way to maintain solitons against attenuation that reduces their intensity below the level needed to sustain them. Researchers knew that what was needed was some form of optical amplifier that would periodically reboost the solitons without changing their shape. In 1987, with the development of erbium-doped fiber amplifiers (EDFAs), this optical amplifier became feasible and in turn made possible the development of long-distance soliton communication systems. In theory, with periodic boosting by EDFAs, solitons could propagate indefinitely without the need for any electronic repeaters (see Fig. 2).The basic advantage of solitons is that they use nonlinearities to automatically preserve and regenerate their pulse shape, while conventional linear approaches have to fight nonlinearities and use external regeneration to regain good pulse shapes. Because solitons preserve themselves stably, they can be generated automatically out of a nonideal pulse. They can reform themselves after distortion by amplification, or after collision with other solitons. Because they use dispersion, they can operate over a broad band of wavelengths around the attenuation minimum, not merely near a zero-dispersion point.
The rapid development of WDM systems based on linear transmission of pulses has led to near-term plans for systems carrying as many as 16 channels with a total of 160 Gbit/s over 1000 km (see Laser Focus World, July 1997, p. 119). But solitons seem capable of higher performance over the longer distances typical of trans-Pacific fiber connections. In the laboratory, using fiber loops, soliton-based WDM transmission has been demonstrated for four channels of 10 Gbit/s each over 20,000 km. As for single channels, solitons appear to make possible nearly an order of magnitude higher capacity than linear WDM.
Getting rid of the noise
Even with these remarkable properties, there are still obstacles that must be overcome to achieve the highest transmission capacities. One of the most serious is the effect of amplifier noise on pulse timing. In any optical amplifier based on stimulated emission there is always a noise level produced by amplified spontaneous emission. Such noise, when added to a soliton, produces a random shift in the central frequency of the soliton.
Because the central frequency is related to the velocity of the soliton through the fiber, random shifts in frequency produce change in velocity and eventually jitter, in which pulses can be shifted out of their proper position. This noise-induced jitter is termed the Gordon-Haus effect. For higher bit rates, a smaller jitter will cause a pulse to overtake a neighboring one, so the Gordon-Haus effect tends to limit the maximum bit rate to around 5 Gbit/s for trans-Pacific transmission.
Another source of jitter is the influence of each soliton on its neighbors. Solitons of the same phase tend to attract each other, and two isolated solitons will oscillate around each other, passing through each other periodically in a bound state. While a train of equally spaced solitons will be stable against these sorts of oscillations because the force on each soliton will be balanced, a signal in which the presence or absence of a soliton signifies a 1 or 0 will generate unbalanced forces for many solitons. If these are sufficient, they can cause solitons to exchange places. The only cure for this is to ensure that solitons are kept at least several pulse lengths apart from one another, meaning that in practice transmission at 20 Gbit/s requires pulses shorter than 10 ps.
When soliton channels on different wavelengths are combined in a WDM system, other problems arise, because the pulses at different wavelengths travel at different velocities, and thus collision between solitons of different wavelengths is inevitable. Normally such collisions do not affect the solitons, which reshape themselves automatically. If, however, the collision takes place while the solitons are passing through a fiber amplifier, distortions can result in jitter, which tends to set a limit on the how close in wavelength channels can be and on the total number of channels.
Guiding filters
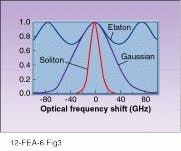
The basic method for overcoming these limitations of soliton bit rates is through narrow-band etalon filters, or guiding filters. If the filter is sufficiently narrow and is centered on where the soliton center frequency should be, noise-induced shifts in that frequency will be filtered out, restoring the soliton to its proper frequency and preventing jitter (see Fig. 3). Naturally, a narrow-band filter will filter out some of the soliton`s own frequency components, but part of the beauty of solitons is that, unlike other shaped pulses, they will automatically regenerate their missing frequencies.Guiding filters with a fixed frequency can cut Gordon-Haus jitter roughly in half. However, some jitter remains, as additional amplification must be provided to compensate for the losses caused by the filter, and noise at frequencies close to the filters peak will become amplified with time.
A second idea, credited to Mollenauer, gets rid of this problem by "sliding" the frequency of the filters down the length of the fiber. Each filter shifts to a slightly higher frequency than the one before it, so that noise amplified by one filter will be filtered out by the next. The solitons, curiously enough, will simply shift their central frequency to follow the filters’ central peaks. In this way, the solitons will be transmitted through the sliding filters, but the linear noise will not.
Not only do sliding-frequency filters eliminate nearly all Gordon-Haus noise, but they radically reduce the noise generated by soliton collisions as well in WDM systems, allowing closer spacing of communications channels. In addition, these filters are less costly to implement than fixed-frequency filters because the frequencies do not have to be accurately matched but merely have to be within a certain band.
The rapid pace of soliton research in the laboratory appears to guarantee that the phenomenon Russell looked on a century and half ago as a curiosity will, in not too many years, be carrying millions of phone conversations across the oceans.
FURTHER READING
J. M. Arnold, "Solitons in Communications," Electronics Communications Engineering Journal, p. 88 (April 1996).
K. C. Chan et al., "Application of Optical Solitons," Journal of High Speed Networks 4, p. 41 (1995).
L. F. Mollenauer, J. P. Gordon and P. V. Mamyshev, "Solitons in High Bit-Rate, Long Distance Transmission" in Optical Fiber Telecommunications, Volume IIIA, p. 373 (1997).
About the Author
Eric J. Lerner
Contributing Editor, Laser Focus World
Eric J. Lerner is a contributing editor for Laser Focus World.