Entangled photons beat the diffraction limit
Ever since the discovery that the resolution of optical instruments is limited by the diffraction of light, engineers have tried to push that limit. For example, a well-known rule of thumb in microscopy is that two object points spaced by a lateral distance s are well resolved under a microscope if s is greater than λ/NA, with λ being the wavelength of the imaging light and NA being the numerical aperture of the microscope. Hence, lowering λ and increasing NA have been the main routes to resolution improvement.
Using lasers to "tailor" light opens opportunities for better resolution improvement, for example by the reduction of the point-spread function in fluorescent samples by stimulated-emission depletion, or in confocal fluorescence microscopy by two-photon excitation.
A scheme to use entangled photons is being investigated to achieve the simultaneous arrival of two photons, which increases the two-photon-fluorescence excitation yield.
Entangled photons exist in a common quantum state. They originate simultaneously, are locally well defined in an elementary event, and can subsequently take different paths without "forgetting" their mutual quantum correlation. The result of a quantum-state measurement applied at one photon reveals in a unique way the entangled quantum state of the other photon. But entangled photons have a second property apart from simultaneous generation that renders them highly interesting for resolution improvement in interferometry, metrology, and imaging.
In 1995, researchers from Stanford University theoretically described the interferometric behavior of a number N of photons of wavelength λ in a definite quantum state (Fock state), finding that N photons in a quantum state exhibit an "effective wavelength" λ/N.1 This aspect is of great interest for interferometric applications: by combining N photons in a definite quantum state and using solely light in this state, resolution should become scalable with the number N of photons in a wave packet.
But how can such pure states be realized? Several groups have realized and investigated bi-photon states using the well-known spontaneous parametric downconversion in nonlinear crystals, which supplies, in the degenerate case, two entangled photons of wavelength twice that of the incident photon. Indeed, in two-photon coincidence measurements, the λ/2 nature of the interference pattern could be shown. To improve resolution, however, three or more photons must be used when they have been generated at first by parametric downconversion, and the resulting interference pattern must not be washed out by a superposition of lower-order contributions at longer wavelengths.
Polarization-entangled photons
This result has been realized by two groups, one at the University of Vienna and the other at Toronto University.2, 3 The Vienna group, led by Anton Zeilinger, used so-called type-II spontaneous parametric downconversion. This method directly supplies two energy-degenerate polarization-entangled photons from a nonlinear crystal—one polarized ordinary (vertical), the other polarized extraordinary (horizontal) with respect to the crystal. The photons are emitted onto separate cones, the two of which can be made to intersect along two lines, yielding two beams in one polarization-entangled state.
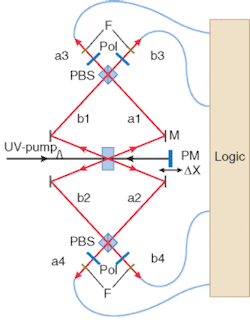
FIGURE 1. In a setup for the generation of two- and four-photon states, a UV beam passes through a BBO crystal and is reflected at a mirror PM so that one or two pairs of entangled photons are generated, one pair taking the a 1, 2 modes of propagation, the other the b 1, 2 modes. The generation of a single pair can happen either before or after reflection so that either a 1, 2 or b 1, 2 is followed. The polarizing beamsplitters PBS pass horizontally polarized photons and reflect vertical ones, thus combining the a 1, 2 and b 1, 2 propagation modes in the a 3, 4b 3, 4 sections. Polarizers set to 45° provide indistinguishability of H and V polarizations at the detectors. Two pairs of photons can be generated during forward, backward, or both pump passages, feeding both a 1, 2 and b 1, 2. Adjustment of the setup provides spatial and temporal overlap of pairs in a 3, 4b 3, 4 sections.
For pumping, a 790-nm laser was modelocked and frequency doubled. The 395-nm beam passes through a BBO (beta barium borate) crystal and is reflected at a mirror (see Fig. 1). Either single pairs or two pairs of photons can be generated. Narrow spectral filtering in all channels selects monochromatic photon pairs, effectively "engineering" a four-photon state out of two physically generated two-photon states. The probability for single-pair generation is between 10-2 and 10-3, while that for double-pair production is 10-4 to 10-6.
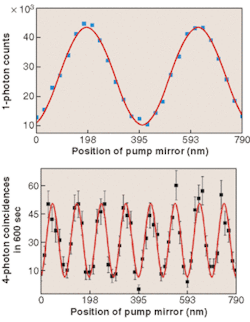
The apparatus allows operation as a Mach-Zehnder interferometer with single-channel detection, and double- and four-channel two- and four-photon coincidence detection, all at 790 nm (see Fig. 2). The resolution of the four-photon trace is improved by a factor of four. The authors determined that the four-photon trace is not an artifact due to two two-photon interferences. In principle, this scheme can be extended to the creation of even more entangled photons.
The Toronto group, led by Aephraim Steinberg, used a photon pair from type-II parametric downconversion in collapsed-cone geometry, adding one laser photon to generate a three-photon entangled state. Their threefold coincidence signal demonstrates a threefold resolution improvement. The authors claim that their method should allow construction of multiphoton states from a priori unentangled photons.
REFERENCES
- J. Jacobson et al., Phys. Rev. Lett. 74, 24 (1995).
- P. Walther et al., Nature 429 (2004).
- M. W. Mitchell et al., Nature 429 (2004).