Ten-femtosecond amplifier creates multiterawatt pulses
Ten-femtosecond amplifier creates multiterawatt pulses
High-order phase compensation and regenerative pulse shaping could propel amplified ultrashort pulses to petawatt-level peak powers.
Christopher P. J. Barty
Is it possible to produce a petawatt (1000 terawatts) laser pulse of only a few optical cycles in duration? Could a laser system that produces such pulses operate at a repetition rate of many hertz and with diffraction-limited beam quality? Could a kilohertz repetition source be built that produces multiterawatt pulses?
Answering affirmatively to these questions would have been almost unthinkable only a couple of years ago. However, with the emergence of Ti:sapphire as a high-quality, ultrabroadband-amplification material and of two new technologies that enable chirped-pulse amplification (CPA) to be performed at the 10-fs level (see photo at right), it is now not only possible to conceive of such systems, but the components needed to construct them exist today.
Over the last 10 years, CPA has become the technique of choice for producing high-peak-power, ultrashort-duration optical pulses.1 By chirping--that is, distributing the frequency content of the pulse in time--a low-energy, short-duration seed pulse can be expanded to a significantly longer duration. Amplification of this longer-duration pulse can occur at high fluences (energy per unit area) without resulting in intensity-dependent damage of the amplifier components. After amplification, the chirp can be removed with an appropriate dispersive delay line, and a high-peak-power, short-duration pulse is produced. In theory, the duration of the recompressed pulse can be the same as the initial unchirped seed pulse, and the peak-power increase can be equal to the ratio of the chirped-pulse duration divided by the initial seed duration, or greater than 1000-fold.
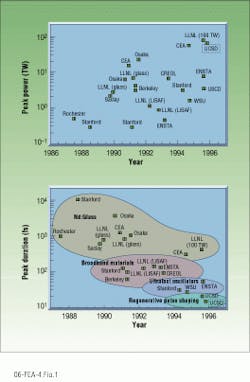
Peak powers from CPA systems have steadily increased (see Fig. 1, top) from less than a terawatt initially to a present record of 125 TW. Table-top systems that can produce peak powers equivalent to the largest national-laboratory-scale Nd:glass amplifier chains are not uncommon. At the same time, pulse durations from CPA systems have steadily decreased from greater than 1 ps to a current record of 18 fs (see Fig. 1, bottom).
As research tools, the extremely short-duration (<100 fs) systems have two intrinsic advantages over other sources of high-peak-power pulses. Much less energy is required to reach the same peak power, and thus the repetition rate of the systems can be many hertz. As a result, the number of terawatt-level pulses that can be produced and used in an experiment each hour is unprecedented. For instance, a single arm of the world`s largest laser system, the Nova laser at Lawrence Livermore National Laboratory (Livermore CA), produces pulses of about 10-TW peak power (10 kJ in 1 ns) at a rate of up to 1 shot per hour. A 10-TW laser system based on amplification of a 10-fs pulse to the 100-mJ level can have a repetition rate of greater than 10 Hz, or more than 36,000 shots per hour.
Sub-100-fs multiterawatt lasers have led to the rapid study and application of a variety of high-field phenomena including novel field-driven XUV lasers,2 ultrafast incoherent x-ray generation,3,4 and high-order harmonic generation.5 In addition, because the amplified energy is modest, that is, less than 1 J, it is possible to maintain nearly diffraction-limited beam quality throughout the amplification process. A 10-fs-range, 100-TW diffraction-limited laser pulse would be capable of producing a focal intensity of greater than 10 zetawatts/cm2 (1022 W/cm2). The corresponding peak electric field at this intensity is on the order of 300 teravolts/m; this value is more than six orders of magnitude greater than the largest gradient that has been used for high-energy particle acceleration. The photon pressure at this intensity is approximately 1012 atm or 10 times higher than that used to initiate a thermonuclear explosion.
Because light travels only 3 µm in 10 fs, the focal volume--the product of the transverse focal-spot size and the longitudinal spatial extent of the pulse at the focus--could be on the order of 10-12 cm-3, or a volume roughly equivalent to that of a small bacterium. As a result, the energy density at the focus could be greater than 1011 J/cm3 or nearly 12 orders of magnitude larger than that produced by one beam of the Nova laser system. This energy density is also equivalent to that produced by a 150 million degree blackbody (our sun is a ~5000° blackbody). Laser/matter interactions at these intensities and energy densities on these time scales have never been studied and may lead to new compact particle accelerators, ultrashort-wavelength x-ray lasers, ultrahigh-density plasmas, attosecond VUV pulses, highly ionized dense atomic clusters, and probably to new and unanticipated phenomena.
High-order phase compensation
The generation of a 10-fs-range, multi terawatt pulse is complicated by many considerations that are not important in longer-duration CPA systems.6 The most critical of these are phase and amplitude distortions that occur during the amplification process. These distortions become rapidly more severe as the duration of the seed pulse decreases and have been the principal reasons why 10-fs-level CPA has been a tremendous challenge.
A 10-fs optical pulse has a spectrum that spans an extremely wide range. Pulses from modelocked, Ti:sapphire oscillators can have bandwidths in excess of 100 nm FWHM. Only when each spectral component of this bandwidth has the same relative phase, does each add constructively and result in the shortest possible pulse duration.
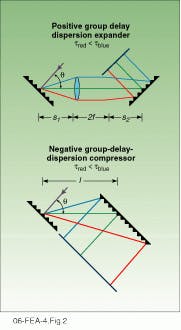
It is very easy for this condition to be destroyed. For instance, the dispersion caused by propagation through only 1 mm of optical glass is enough to cause a 10-fs pulse to broaden in time to 20 fs. Of course, in CPA systems dispersive optical arrangements are used intentionally, first to delay the different spectral components with respect to one another, thus allowing a long-duration seed pulse to be created before amplification and second to recompress the pulse after amplification (see Fig. 2).
To first order, these arrangements produce a linear delay of frequency with respect to time whose magnitude is proportional to the separation of the gratings in each arrangement and whose sign is opposite--positive for the expander and negative for the compressor. In addition, the material in the amplifier chain (Pockels cells, polarizers, and gain media) to first order also produces a positive linear delay of frequency with time. Thus, the combination of the expander dispersion, material dispersion, and compressor dispersion can be exactly balanced to give equal delay for each frequency after amplification and thus can create a transform-limited short-duration pulse.
However, as the bandwidth of the seed pulse increases and/or the duration to which the seed pulse is stretched before amplification increases, the spectral delays of the expander, compressor, and material all deviate from ideal linearity. In this case, it is generally not possible to have equal delay for all frequency components through the laser system and to produce a transform-limited pulse. It is possible, however, to circumvent this problem with an expander designed to allow for control of higher-order nonlinearities in spectral delay.
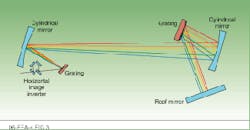
For seed pulses of ~100 fs and stretching ratios of ~1000, transform-limited compression can be achieved if one can compensate for the parabolic deviations of pulse delay from linearity, otherwise known as cubic or third-order phase distortion. For ~10 fs pulses and/or stretching ratios of significantly more than ~10,000, it is necessary to compensate for at least the next order, otherwise known as quartic or fourth-order phase distortions. Quartic compensation can be accomplished with an expander design based on off-axis cylindrical reflective optics (see Fig. 3).7 The combination of spherical aberration introduced by off-axis incidence on the mirrors and angular dispersion caused by the gratings creates a higher-order phase distortion that, for the correct orientation and spacing of its components, can exactly balance the sum of the distortions caused by the material dispersion of the system and the compressor.
Numerical simulations indicate that the net spectral delay after amplification of a multiterawatt, joule-level system that utilizes this pulse expander can be less than 1 fs over a bandwidth of 100 nm, even though the seed pulse is stretched by a factor of greater than 100,000 times. It should be noted that this is accomplished despite the presence of more than a meter of optical material in the amplification chain. In principle, it is possible to scale to higher output energy simply by adding more stages of amplification and then reorienting the expander components to compensate for the additional material dispersion.
Regenerative pulse shaping
In much the same way as it is critical for each frequency component to experience the same delay through the amplification system to produce a transform-limited pulse, it is also critical that each frequency component experience the same net amplification if the pulse spectrum is to remain unchanged and the shortest pulses are to be generated. In general this condition does not occur. The gain cross sections of most gain media have roughly bell-shaped frequency dependencies. Thus, frequency components near the peak of the gain profile will experience more amplification than those further away. This leads to a reshaping and narrowing of the pulse spectrum during amplification.
As the pulse bandwidth comes on scale with the amplifier bandwidth, this gain narrowing becomes significant. In Ti:sapphire this condition occurs for pulses of less than ~50 fs in duration. For a 10-fs bandwidth input pulse and a total small signal gain of 1012, which is typical for a multiterawatt system, the resulting amplified spectrum has a FWHM that is nearly three times narrower and thus can be recompressed to no less than 30 fs in duration. It is possible to overcome this fundamental limitation with a technique that we have termed regenerative pulse shaping.8
Key to this concept is the fact that the total amplification experienced by the pulse occurs as a result of many passes of the amplifier material. The small signal gain on any one pass is modest, typically a factor of two to four, and thus the reshaping of the spectrum per pass is small. As a result, it is possible to compensate for gain narrowing after each pass by introducing a linear filter that has a transmission roughly the inverse of that of the single-pass gain of dependence. This is conveniently accomplished in a regenerative amplifier by placing the filter inside of the amplifier cavity (see Fig. 4).
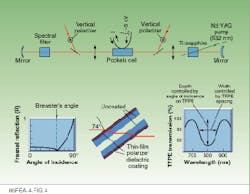
We have investigated a number of possible filters and have developed a new thin-film polarizer etalon (TFPE) that is ideal for ultrabroadband pulse shaping inside of regenerative amplifiers (see Fig. 5). Our regenerative amplifier operates by rotating the input-pulse polarization by 90° with a pulsed half-wave Pockels cell, trapping the pulse inside the cavity until the Pockels cell is fired to a half-wave voltage again some 10 to 12 round-trips later. The thin-film polarizer etalon is used both as the input and output coupler and also as the filter for regenerative pulse shaping.
Filtering is accomplished by spacing the plates of the etalon by an odd number of quarter wavelengths. This produces a transmission that has a minimum at ~800 nm and maxima on either side. The spectral width of this modulation is determined by the spacing and can be adjusted to give a flat gain profile or a gain profile that favors two-color amplification. By placing one-half of the etalon on a piezoelectrically driven translation stage, it is possible to electronically tune the center frequency and bandwidth of the amplified pulse spectrum in real time.
The major advantage of the TFPE is that the angle of incidence of the pulse on the inner etalon-forming surfaces of the device is much larger than Brewster`s angle. As a result, the Fresnel reflection of each surface is much greater than at normal incidence. Using Alpine Research Optics (Boulder, CO) thin-film polarizer coatings on the outer surface, we are able to achieve angles of incidence of at least 74°.
With a combination of these devices and a modified regenerative amplifier, amplified bandwidths of ~120 nm, or nearly four times the theoretical gain-narrowing limit without pulse shaping, have been demonstrated. It is also possible to change the depth of modulation of the TFPE filter simply by changing the angle of incidence of the device. We are currently working with Alpine Research Optics to develop optimized coatings for a number of applications. It is important to note that the dispersion introduced by the etalon effect under the condition of antiresonance (odd number of quarter-wavelength spacing) is a factor of 106 smaller than the dispersion of the expander or compressor and thus does not add any appreciable phase distortion to the system.
Laboratory experiments
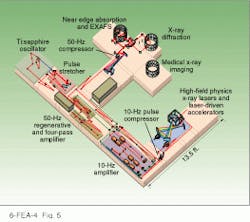
Both regenerative pulse shaping and high-order phase compensation were implemented in two multiterawatt systems at the University of California, San Diego (see Fig. 6). The two systems share a common 9-fs oscillator, cylindrical mirror-based pulse expander, 50-Hz regenerative amplifier, and 50-Hz four-pass amplifier. After the four-pass amplifier, an electro-optic switch selects one pulse out of every five for further amplification in a two-pass, 10-Hz amplifier. Each arm has its own pulse compressor.
Amplification and compression of the 50-Hz system has been performed without the electro-optic switch and has resulted in transform-limited pulses of 4-TW peak power and 18-fs duration.9 This result, however, was obtained with an earlier variation of the filter described above that limited the amplified bandwidth to ~75 nm. It is expected that pulses of ~12 fs will be possible with an optimized regenerative amplifier that includes two TFPEs. Because of the extremely large stretching of the seed pulses (>100,000 times), the amplifiers are operated well above the saturation fluence for Ti:sapphire (~1 J/cm2), and thus it is possible to very efficiently extract the stored energy of the final amplifiers.
Record conversion efficiencies of pump light to 800-nm amplified light of more than 75% of the theoretical maximum have been achieved from the four-pass amplifier. Amplification to the 1.8-J level at 10 Hz has been performed with a portion of the available 10-Hz pump energy, but as of this writing the compressor for this beam has not been completed. With a design goal of ~100 TW in 15 fs these pulses must be compressed in vacuum to avoid nonlinear distortions introduced by propagation in air.
Scaling of the techniques described above to shorter durations, higher peak powers, and higher repetition rates is straightforward and limited primarily by the availability of suitable pump lasers. We are developing a postamplified kilohertz system that could eventually produce terawatt pulses of ~10 fs in duration. The minimum necessary pump energy required is ~30 mJ--a readily achievable value using a combination of commercial sources.
Finally, in principle, petawatt peak-power pulses of 15 fs in duration could be created with a minimum of ~40 J of 532-nm pump light. Diffraction-limited 532-nm pulses in this energy range have recently been demonstrated at a repetition rate of 6 Hz from a phase-conjugated Nd:glass laser.10 The construction of a 15-fs, multihertz, petawatt source based on the techniques described above has recently been budgeted for construction over the next five years by the Advanced Laser Sciences Division of the Japanese Atomic Energy Research Institute. n
ACKNOWLEDGMENTS
Ting Guo, Georg Korn, Catherine Le Blanc, Ferenc Raksi, Christoph Rose-Petruck, Jeff Squier, Kent Wilson, Barry Walker, Vlad Yakovlev, and Koichi Yamakawa have all contributed greatly to the construction of the laser systems at the University of California, San Diego, and the development and refinement of the techniques described in this article.
REFERENCES
1. D. Strickland and G. Mourou, Opt. Commun. 56, 219 (1985).
2. B. E. Lemoff et al., Phys. Rev. Lett. 74, 1574 (1995).
3. M. M. Murnane, H. C. Kapteyn, and R. W. Falcone, Phys. Rev. Lett. 62, 155 (1989).
4. J. D. Kmetec et al., Phys. Rev. Lett. 68, 1527 (1992).
5. J. J. Macklin, J. D. Kmetec, and C. L. Gordon III, Phys. Rev. Lett.70, 766 (1993).
6. C. P. J. Barty et al., Proc. SPIE: San Jose, CA, 311 (1995).
7. B. E. Lemoff, and C. P. J. Barty, Opt. Lett. 18, 1651 (1993).
8. C. P. J. Barty et al., Opt. Lett. 21, 219 (1996).
9. C. P. J. Barty et al., Opt. Lett. 21 (May 1. 1996).
10. C. B. Dane et al., J. Quant. Electron. 31, 148 (1995).
Chris Barty adjusts
pulse-compressor
separation to produce
sub-20-fs multiterawatt
pulses at a 50-Hz repetition rate. Focusing this output
in air generates contiuum
radiation (fire-red on left).
FIGURE 1. Representative sampling of abridged history of chirped-pulse amplification (CPA) shows the increase in peak power achieved by various groups (top). Tracing similar development in pulse duration from terawatt-level CPA systems reveals how different technologies impacted experiments (bottom). (Dotted lines enclose projects currently under development.)
FIGURE 2. In conventional chirped-pulse amplification (CPA), expander stretches pulses in time (top) so that the transit time, t, is longer for shorter wavelengths (tred < tblue); compressor shortens pulses after amplification (bottom). Dispersion is matched if and only if these conditions are met: l = 2f - s1 - s2; qexp = qcomp; lenses are paraxial; and there is no material in the system. Small mismatches between the dispersion of the expander, material in the amplification system, and the compressor can lead to large recompression for ultrashort pulses in conventional CPA devices.
FIGURE 3. In cylindrical-mirror-based pulse expanders, the combination of spherical aberration and angular dispersion allows control of high-order dispersion. The pulse is vertically multiplexed with a roof mirror after the second grating and is sent through the entire system twice. To eliminate transverse spatial effects, the horizontal image of the beam is inverted with a four-mirror image-inverter arrangement before the second pass.
Figure 4. Thin-film etalon polarizer (lower center) eliminates gain narrowing in Ti:sapphire regenerative amplifier.
FIGURE 5. Regenerative pulse shaping corrects for gain narrowing on each round-trip with a spectral filter inserted in half-wave regenerative amplifier cavity (top). A thin-film polarizer etalon (TFPE, bottom) provide both high modulation and a means for input and output of the amplified pulse. Thin-film coatings on the outer surface of the etalon have minimum reflection at angles much greater than Brewster`s angle for the substrate material and results in a high Fresnel reflection (left) on the inner surface and a large modulation depth (right). The depth and width of modulation of the filter can be adjusted by changing the angle of incidence and spacing of the etalon, respectively.
FIGURE 6. Two arms of ultrafast laser system at University of California, San Diego, share a 9-fs Ti:sapphire oscillator, cylindrical-mirror-based pulse expander, a 50-H¥regenerative amplifier, and a 50-H¥four-pass amplifier. An electro-optic switch can pick one pulse of five for subsequent amplification in a 10-H¥amplifier; this 10-H¥compressed beam is used in studies of high-field physics, x-ray lasers, and laser-driven accelerators (right); without the electro-optic switch, the 50-H¥train produced 18-fs pulses with peak powers of 4 TW. This beamline is currently being used in various laser-generated x-ray experiments.
CHRISTOPHER P. J. BARTY is director of laser science with the Institute for Nonlinear Science at the University of California, San Diego, La Jolla, CA 92093-0339; e-mail: [email protected].