Laser neural network promises improved pattern recognition
Laser neural network promises improved pattern recognition
Evert Mos, Jean Schleipen,
and Huug de Waardt
An optical neural network experiment has been successfully completed using a single laser diode and external optics by our research team at the Eindhoven University of Technology and the Philips Research Laboratories (Eindhoven, The Netherlands). The longitudinal modes of the laser represented the neurons, and when external optical feedback was applied to the laser diode the set-up behaved like a neural network.1,2
An artificial neuron is a simplified model of a biological neuron. It has a number of inputs and one output, and it performs simple arithmetic operations using the following steps--the inputs to the neuron are weighted and summed, and the weighted sum is compared to a threshold. Depending on the result, the output of the neuron will be either high or low.
A network consisting of a number of such neurons can be "trained" to perform an input-to-output vector function by setting the weight values of all neurons properly. This process of adjusting the neural weights is called the learning phase.
Good feedback
Sensitivity to external feedback is an unwanted effect in laser diode applications such as optical data storage and optical communications. In our neural network, however, we use this nonlinear effect to implement the threshold function for the neurons. The reflectivity of the laser diode mirror at the external feedback side was reduced to maximize this effect.
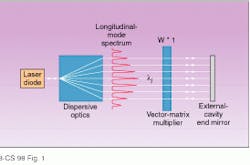
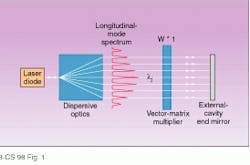
In the external cavity the laser beam was spatially separated into several beams--one for each of the longitudinal cavity modes--by means of dispersive optics. Each of these beams, corresponding to one longitudinal mode, was attenuated individually before being reflected back to the laser diode by the end mirror of the external cavity. The amount of attenuation for each beam, and thus for each longitudinal cavity mode, was therefore proportional to a weighted sum of inputs that was implemented with an optical matrix vector multiplier (see Fig. 1).
In the experimental set-up, two lenses form a sharp image of the active area of the laser chip on the external cavity mirror to obtain maximum feedback. Two gratings provide the dispersion needed to spatially resolve the longitudinal modes of the laser diode (see Fig. 2). The spatial separation between two adjacent modes matches the spacing of the attenuation elements of the optical vector-matrix multiplier. The vector-matrix multiplier (see inset to Fig. 2) is formed by two cylindrical lenses and a passive-matrix liquid-crystal display (LCD). On the LCD an image of four rows and five columns is formed, and each of the pixels can be set to one of 31 discrete gray levels. We used the LCD for adapting the neural weights, as well as to provide the inputs to the network.
Neural training
To train the laser neural network (LNN) to produce a specified output at a given input a supervised learning algorithm was used in which the supervisor fed sample input patterns to the network and simultaneously monitored the output of the network. The weight matrix of the network was changed, using another algorithm, until the supervisor received the desired output pattern for each input pattern. To use such a learning scheme in our experiment a supervisor must set the inputs and weights of the LNN and measure its output vector.
In our set-up a PC was the learning supervisor and controlled the addressing of the LCD via its parallel port. This PC provided the network with four input gray levels and the 4 ¥ 5 gray-level matrix of neural weights. The output was monitored by a second PC, which received the neural outputs from the optical multichannel analyzer (OMA) in integer counts proportional to the optical power in the longitudinal cavity modes. In each learning trial, the outputs were read by the second PC and sent to the supervisor PC, in which a stochastic learning algorithm changed the weights of the network randomly until the difference between actual and desired output vectors was below a preset level for all input patterns.
The feedback of each of the longitudinal modes was controlled separately, and the optical power contained in each mode exhibited neural behavior. In this manner a neural network was formed in which the optical powers of the longitudinal cavity modes of the laser were the outputs of the network. The optical neural network thus constructed had a single-layer architecture with as many neurons, in principle, as there were longitudinal cavity modes. Due to the longitudinal-mode competition commonly found in multimode lasers, connections between the neurons arose. These connections were inhibitory--an increase in the optical power contained in one mode caused a decrease in the optical powers of the other modes.
By measuring the relation between the sum of weighted inputs and the output levels of a set of neurons, the neural activity of our set-up was demonstrated. In the LNN, the sum of weighted inputs for a specific neuron corresponded to the total transmission of its LCD-column while the output levels of the neurons were represented by the optical powers contained in the cavity modes.
The stochastic learning algorithm was used to make this network perform (digital) input-output functions of up to three inputs and five outputs. One of the training examples was based on the NOR/XOR/AND function. Although most of the training examples were trivial, some of them could be useful in practical systems, such as demultiplexing optical communication data or checking message parity.
In future experiments, more-complicated learning tasks will be trained to the network to examine the performance of the LNN in practical applications such as pattern recognition (see "Optical domain holds advantages for neural networks," p. 132). Improvements in speed and multidimensional capability will be needed, as well as an ability to control the input vector optically instead of electronically. The current experiments show, however, that the network has good stability and can be trained with good reproducibility. o
REFERENCES
1. S. B. Colak, J. J. H. B. Schleipen, and C. T. H. Liedenbaum, IEEE Transactions on Neural Networks; in press.
2. J. J. H. B. Schleipen et al., Fourth int. conf. on
microelectronics for neural networks and fuzzy
systems, Turin, Italy, 8 (1994).
FIGURE 1. Laser diode in laser neural network setup has an external cavity to provide feedback. Dispersive optics are used to spatially separate the light beams of the longitudinal modes; a vector-matrix multiplier makes the optical feedback proportional to a sum of weighted inputs for each of the longitudinal modes.
FIGURE 2. In experimental setu¥for laser neural network (LNN), lenses L1 and L2 form an image of the laser diode`s exit facet on mirror M. Gratings G1 and G2 disperse the longitudinal cavity modes (l1Ul5) of the laser diode. Inset shows optical vector-matrix multiplier in the external cavity. Lenses L3 and L4 distribute the power over the rows of the LCD. I represents the input vector, and W represents the weight matrix. The figure also shows the training system. The zeroth order of G1 is coupled into a fiber and analyzed by the optical multichannel analyzer (OMA). The first PC (PC-1) receives the output values of the LNN through a second PC (PC-2), connected to the OMA.
Optical domain holds advantages for neural networks
In the development of artificial neural networks, software has played an important role, because classical (sequential) computers use the parallelism of computation only as a concept. The use of dedicated neural hardware would therefore lead to an increase of computational speed, and various neural circuits have been realized on silicon.1 For several reasons, the optical domain presents a more suitable candidate for implementing neural networks.
First, light beams cross each other in free space without interacting. Second, all three dimensions can be used, which reduces the problem of interconnectivity and allows for larger and more-complex networks. Third, optical systems are potentially much faster at weighting and summation because speed limitations due to charge build-up, as in electronic systems, are not present.
These obvious advantages of using optics for processing data are illustrated by the fact that numerous optical neural networks, and in general optical computing experiments, have been demonstrated in the past five to ten years.2-7
REFERENCES
1. D. Hammerstrom and S. Rehfuss, Artificial Intelligence Review 7(5), 285 (1993).
2. A. Jennings, P. Horan, and J. Hegarty, Appl. Opt. 33(8), 1469 (1994).
3. A. Hirose and R. Eckmiller, Appl. Opt. 35(5), 836 (1996).
4. B. Javidi, J. Li, and Q. Tang, Appl. Opt. 34(20), 3950 (1995).
5. I. Saxena and E. Fiesler, Opt. Eng. 34(8), 2435 (1995).
6. S. Juthamulia and F. T. S. Yu, Opt. and Laser Techn. 28(2), 59 (1996).
7. F. T. S. Yu, Progress in Optics 32, 61 (1993; E. Wolf, ed., North Holland Physics Publishing Co.).
EVERT MOS is a PhD student at Eindhoven University of Technology, JEAN SCHLEIPEN is a researcher at Philips Research Laboratories (Eindhoven), and HUUG DE WAARDT is an associate professor at Eindhoven University of Technology, POB 513, 5600 MB Eindhoven, The Netherlands.