Laser Optics: Monolithic afocal beam expanders provide flexible capability
ULRIKE FUCHS
Passive optical components are indispensable in complex laser systems such as those used in materials processing, and to nearly all lab applications as well. Matching an incoming beam diameter (1/e2) to the diameter required by the downstream system is a common task, where Galilean-type telescopes are preferred for beam expansion.
Researchers and customers have, however, come across a large number of limitations in the use of these systems. They are too complicated to adjust, require a very narrow incoming beam diameter, and are too inflexible in terms of magnification. In addition, the property of diffraction-limited performance can sometimes only be maintained within the framework of the optical design and not in the actual construction of the beam-expansion system. So, a preferred system would be adjustable for the wavelength being used without varying the magnification. Galilean-type beam expanders generally have chromatic properties that necessitate adjusting magnification when changing the wavelength.
Monolithic aspheric beam expansion
Monolithic beam-expansion systems use a somewhat different approach from that of conventional systems based on the Galilean telescope. While their function is still similar to the Galilean telescope, they are composed of only a single optical element—a meniscus lens. This principle has been known for a long period of time, but can lead to strong spherical aberrations in its original design with two spherical surfaces, and can therefore only be used for incoming beams with very small diameters and enlargements (see Fig. 1a).
This kind of optical element becomes of particular interest when one of the two surfaces is made aspherical. Such a surface allows for the correction of spherical aberrations and the creation of an afocal system that has use with incoming beams that have large diameters. The enlargement is M=2 in both cases, with an incoming beam diameter of 10 mm.
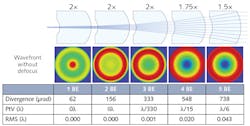
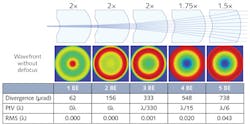
The individual beam enlargements for monolithic Galilean telescope elements are relatively small because of the limited center thickness. As these are afocal beam-expansion systems, they can be placed in series as a means of gradually enlarging the incoming beam along its path (see Fig. 1b). This opens up entirely new possibilities: with only three of these elements, the incoming beam diameter can be increased eightfold, and with five elements even 32-fold.
If individual elements at M=2 are used, the increments for possible enlargement are M=2, 4, 8, 16, 32, and so on. This is an optimal solution when a high level of enlargement is needed within the smallest possible amount of space and a high wavefront quality. If, however, even smaller increments are required, other individual element enlargements in close proximity to one another are needed. Two lower levels at M=1.5 and M=1.75 in particular are provided.
The meniscus lens can be adjusted in both directions along the beam's path, thanks to the afocal dimensioning of the individual elements (see Fig. 1b, part [c]). This means that when they are combined, six—not just three—individual element enlargements are possible, which considerably increases the number of possible combinations. When elements are available for every basic type of enlargement, this allows for a total of 13 possibilities in terms of overall enlargement using only these three meniscus lenses. This combination can be expanded to include other elements, with the use of up to five elements—leading to 230 possible combinations and enlargement increments, of which the largest is M=32.
Use of monolithic beam-expansion systems in a cascade design offers considerably more optical surfaces than conventional Galilean-type systems, which makes every other surface aspherical. For this type of cascade system to be applicable in practice for a flexible beam-expansion system, surfaces of very high quality are required. To avoid later restrictions on the combination of the elements, each individual element needs to be significantly better over its whole clear aperture than the requirement for being diffraction-limited, which is a root-mean-squared (RMS) wavefront error of <λ/14. Consequently, for a Ti:sapphire laser wavelength of 780 nm, the RMS wavefront error must be <55 nm, and for the second-harmonic Nd:YAG wavelength of 532 nm, the RMS error must be <32 nm.
If the center thickness and the decentering of surfaces are implemented with great precision to meet these requirements, the system can be operated without any necessary adjustments since all adjustment degrees of freedom are already set at an optimum as a monolithic element during manufacturing. The addition of further monolithic elements to change the magnification level can thus occur without need of any adjustment, and is fast and uncomplicated as a result.
To demonstrate the performance, wavefront maps of a monolithic beam expander with M=2 at wavelengths of 1064 and 532 nm were measured. In both cases, the RMS wavefront error was 0.018 λ. A measured wavefront map of a five-element set of monolithic beam expanders with M=21 showed an RMS wavefront error of 0.040 λ (0.220 λ P-V), making this cascade system diffraction-limited.
Changing the wavelength: Waveλdapt
In the installation of a conventional beam-expansion system, the distance between the two lenses can be adjusted to compensate for the change in their focal lengths caused by a change in the wavelength. No compensation can occur when monolithic elements are used for beam expansion (see Fig. 2), as the center thickness is not adjustable. The output beam is therefore either divergent or convergent with the use of a monolithic beam expander for a wavelength other than the design wavelength. Wavefront errors of a higher order also occur, as the center thickness diverges from the actual design.The effects worsen further if a cascade of monolithic beam expanders is used (see Fig. 2). The wavefront errors accumulate and the aberration increases more than tenfold—the figures given apply only to the optical design itself. Things become worse when production tolerances are taken into account in this analysis. Although the design analysis for both the RMS and the peak-to-valley (P-V) wavefront errors provides a figure that would be adequate for diffraction-limited operation, one cannot expect such a system to actually achieve limited diffraction in practice.
Since it is not possible to produce monolithic beam expanders for all conceivable wavelengths, a further component is absolutely essential to compensate for all the effects arising from a departure from the design wavelength. The task of designing this is no trivial matter. There are 230 possible combinations of the five elements and the result also needs to be easy to use. Therefore, the goal was to bring about an optical system that represents an expansion to monolithic beam expanders and can be adapted in a way that minimizes the aberration of the output laser beam and automatically reduces imaging errors to the tolerable level, while the beam diameter is kept constant. So, the system is a zoom lens meant to maintain a constant magnification of 1x.
We have called this optical system, which compensates for all effects because of changes in wavelength, Waveλdapt (see Fig. 3a). Its operating principle is deliberately kept simple to make it easy to use. If the "wrong" wavelength is used with these monolithic beam expanders, the most obvious effect is a divergence of the beam from its intended collimation. This is easy to recognize by measuring the beam diameter right behind the beam expanders and then at a further distance (2–4 m). Once the Waveλdapt is added to the beam expanders, it can be adjusted easily by turning one part, and the change in the divergence is then determined through another measurement of the beam diameter until it is the same at both distances.One of the design goals was to keep the magnification constant, even as the lenses change their position, as a means of correcting for a variety of wavefront aberrations and divergence. The result of this rather unusual task for a zoom lens is shown in Fig. 3b. As is illustrated there, the magnification varies according to wavelength and for each beam expander combination. There is a 1% maximum divergence from 1x, which is still within the tolerance allowed for most practical applications. The large green area indicates that the deviation is kept mostly under 0.4%.
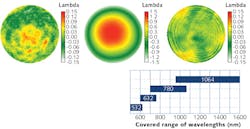
The optical design of the Waveλdapt is created in a way that, when obtaining a collimated beam, it compensates the proper amount for aberrations so that the wavefront is diffraction-limited in the real world.This also means that the theoretical figures are much tighter so that the Waveλdapt has to be placed at the point of the greatest beam diameter to work as required. Figure 4a shows examples of measured wavefronts for two different wavelengths, using the basic configuration with beam expanders at 780 nm and including a Waveλdapt. It is of particular note that this combination has an even lower RMS wavefront error, as intended in the optical design.
Figure 4b shows the spectral range that can be covered with four different Waveλdapts, each designed for a different basic beam-expander wavelength (532, 632, 780, and 1064 nm). Now, it is possible to cover the entire spectral range from 500 to 1600 nm with only these four configurations, which provides for great flexibility in practice—especially since the entire length of the system is much shorter compared to conventional systems.
Ulrike Fuchs is head of applications at Asphericon, Jena, Germany; e-mail: [email protected]; www.asphericon.com.