Frequency Combs: Phase-stabilized ultrafast lasers signal new era in measurement and research
TARA M. FORTIER, ALBRECHT BARTELS, AND SCOTT A. DIDDAMS
The development of short-pulse lasers has progressed steadily over the past 30 years, and during the 1990s the search for better techniques and materials to generate ever shorter pulses delivered Kerr-lens modelocked Ti:sapphire lasers as the system of choice for many applications.1
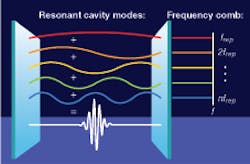
With the broadest gain bandwidth of any conventional lasing material, Ti:sapphire can support the oscillation of millions of coherently related frequencies. In a modelocked laser, the cavity modes have a fixed phase relationship and add together coherently such that the Fourier superposition results in a very strong amplitude modulation of the optical carrier wave. With sufficiently broad gain bandwidth, this modulation is so strong that all of the light waves add up constructively for time periods on the order of a few femtoseconds. The resulting ultrashort pulses repeat at a periodic interval determined by the roundtrip travel time of the pulses inside the laser cavity-typically 1 to 20 ns (see Fig. 1).
Because all of the energy in the light waves is concentrated in such a short time interval, the pulses achieve high peak powers (approximately 1 MW). In the research field of ultrafast phenomena, applications of these lasers have traditionally been twofold: use of the large peak power for nonlinear optics and time-domain applications that take advantage of the femtosecond resolution.
At the end of the 1990s, a lesser-known (perhaps overlooked) application of pulsed lasers came to the forefront-the use of the discrete comb-like character of the modelocked laser spectrum for high-precision optical frequency metrology.2 By combining the techniques of single-frequency laser stabilization and the tools of ultrafast science, scientists are now able to simultaneously stabilize the frequencies of the optical modes emitted by the Ti:sapphire laser. As a result, the phase-stabilized modelocked laser, which can coherently connect optical and microwave frequencies, also became capable of providing a table-top absolute optical frequency reference, replacing the much larger and more complex existing technology of harmonic frequency chains.
These developments have also had significant consequences for the ultrafast-phenomena community. The ability to stabilize all frequencies emitted from the laser simultaneously yields control of the electric field, and hence the phase evolution of the laser light pulses as measured relative to the intensity envelope. The phase stabilization of modelocked lasers has resulted in several exciting new developments in the observation of phase-sensitive nonlinear processes.
With the new applications of these emerging fields came a new wave of development of Ti:sapphire lasers culminating in the development of highly stable and extremely broadband light sources. Such lasers are sometimes referred to as “octave spanning” because the usable spectrum contains frequencies that span an octave in optical bandwidth.
Kerr-lens modelocking
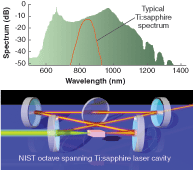
The Ti:sapphire crystal is an ideal candidate for use in broadband lasers, given its large optical gain bandwidth (700 to 1000 nm). Accessing the entire bandwidth, however, is not trivial because the dispersion of the materials in the laser (laser crystal, conventional mirrors, air) causes different optical frequencies to travel at different speeds. The net effect of dispersion is that fewer modes participate in the modelocking process and subsequently decrease the laser pulse bandwidth and peak intensity. Minimizing the effects of dispersion is imperative because high intracavity pulse intensities are necessary for maintaining the strength of the Kerr-nonlinearity, which is the mechanism responsible for modelocking and is ultimately used to maximize the laser bandwidth.
Two methods are commonly used to minimize intracavity dispersion. The first is to place a pair of prisms inside the laser cavity using a geometry that causes red light to travel a longer optical distance than blue light, thus compensating for the positive dispersion of the laser crystal. As an alternative to prisms, “chirped” dielectric mirrors can be used. These mirrors consist of a stack of dielectric layers with varying (chirped) quarter-wave thickness, which allow longer wavelengths to be reflected from deeper within the dielectric coating than shorter wavelengths. The first octave-spanning lasers that were demonstrated used a combination of chirped mirrors and intracavity prisms.3, 4 More recently developed octave-spanning lasers use only chirped mirrors (see Fig. 2).5 Because the dispersion management comes from the laser mirrors alone, the laser cavity can be made quite small (less than 30 cm roundtrip cavity length), resulting in pulse repetition frequencies of more than 1 GHz.When producing a broadband laser, the choice of reflection bandwidth for the cavity mirrors is also important for harnessing as much optical bandwidth as can be produced by the laser. Our laser mirrors are high reflectors, covering a bandwidth slightly greater than that of the Ti:sapphire gain profile. We also use a low-transmission-output coupler (1% from 700 to 900 nm), to maintain high intracavity pulse intensities over the crystal gain bandwidth while out-coupling the wings of the laser spectrum. Finally, to enhance the effect of the Kerr nonlinearity, one of the fold mirrors in the laser has a slightly convex radius of curvature, which helps to enhance the nonlinearity in the cavity. When pumped with 8.5 W at 532 nm from a solid-state pump source, our Ti:sapphire laser produces 900 mW of modelocked laser light. By managing dispersion in the laser cavity and optimizing the intracavity pulse intensity, the nonlinear effects in the laser crystal can be made so strong that the bandwidth is in excess of the gain bandwidth of the laser crystal (see Fig. 2).
Stable light
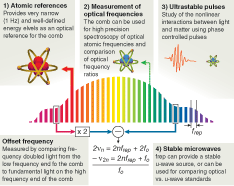
An entirely new range of applications is enabled by recognizing that the resulting optical spectrum, while seemingly complicated, actually consists of a vast array of evenly spaced optical frequency modes, and that the resulting frequency comb can be rigorously defined by only two microwave frequencies. The first frequency is the laser repetition rate, frep, which defines the comb mode spacing and is determined by the laser cavity length. The second is the carrier-envelope offset frequency, f0, which defines the absolute comb position and is determined by dispersion in the laser cavity.2 Stabilizing these two parameters allows production of a laser that emits more than105 optical frequencies, vn, each of which is determined absolutely by the equation, vn = nfrep + f0, where n is the mode number (about 105) that multiplies frep up from microwave into optical frequencies. Conversely, the mode spacing can be seen as the key that provides the approximately 105 division from optical down to microwave frequencies for the direct counting of optical cycles.
The simplest stabilization schemes for the laser offset frequency require an optical octave of bandwidth that is commonly obtained by coherently extending the Ti:sapphire laser bandwidth using special nonlinear fibers.6 Some of the difficulties associated with these fibers are circumvented by octave-spanning lasers, which directly provide the necessary spectral bandwidth to easily measure fo (see Fig. 3). With fo stabilized using standard phase-locked loop techniques, frep can then be precisely controlled by stabilizing one tooth of the comb to an optical frequency reference. A very narrow atomic transition with a natural linewidth of approximately 1 Hz can provide an excellent optical reference in terms of accuracy and stability. Good engineering of the feedback loop for the Ti:sapphire laser permits the transfer of the accuracy and stability of such an atomic standard to every line of the optical comb.
The Ti:sapphire laser stabilized in this manner provides a high-resolution optical ruler that can be used to generate extremely low-phase-noise microwave signals, for performing high-precision spectroscopy and for the comparison of different optical and microwave clock transitions (see Fig. 3). Indeed, the impact of this technique for precision physical measurements and spectroscopy was recognized in the 2005 Nobel Prize for physics.2 Atomic clock comparisons, which provide relative frequency measurements with fractional levels below 10-15 have garnered increased attention. With the increasing measurement sensitivity, laboratory-based comparisons of atomic clock transitions are now providing tests of fundamental postulates of physics, including searches for possible temporal variations of fundamental constants.REFERENCES
1. An excellent review of the progress in this field is found in Ultrafast Phenomena (published by Springer), which are the proceedings of the biennial conference with the same name, most recently held in Niigata, Japan (2004).
2. This optical-frequency-comb technique was part of the citation for the 2005 Nobel Prize in Physics, awarded jointly to R. Glauber, J. Hall and T. Hänsch. See http://nobelprize.org.
3. R. Ell, U. Morgner, F.X. Kärtner, et al., Opt. Lett.26(6) 373 (March 2001).
4. T.M. Fortier, D.J. Jones, S.T. Cundiff, Opt. Lett.28(22) 2198 (November 2003).
5. T.M. Fortier, A. Bartels, S.A. Diddams, Opt. Lett. 31(7) 1011 (April 2006).
6. H.R. Telle, G. Steinmeyer, A.E. Dunlop, J. Stenger, D.H. Sutter, U. Keller Appl. Phys. B 69(4) 327 (1999).
7. S.G. Karshenboim and E. Peik (Eds.), “Astrophysics, Clocks and Fundamental Constants,” Series: Lecture Notes in Physics 648, XVIII, 346 p. 120 ISBN: 3-540-21967-6 (2004).
TARA FORTIER is a postdoctoral fellow at Los Alamos National Laboratory, Physics Division P-23, Los Alamos NM 87545. ALBRECHT BARTELS is CEO at Gigaoptics, Blarerstrasse 56, 78462 Konstanz, Germany. SCOTT DIDDAMS is a physicist at the in the Time and Frequency division at the National Institute of Standards and Technology; e-mail: [email protected]; www.boulder.nist.gov.