Photonic Frontiers: metamaterials - Metamaterials do optical wonders
You can’t always get what you want—but sometimes you can make it for yourself. Natural materials offer only a limited range of optical properties, but now a new family of artificial “metamaterials” is promising a range of optical properties far beyond anything available in nature.
These new materials consist of many small elements assembled into regularly spaced arrays. The interaction of electromagnetic waves with such metamaterials depends on the shape, composition, and arrangement of the elements-features that developers can adjust to get the desired properties. If the wavelength is large compared to the elements and their spacing, the waves interact with the metamaterial as if it had uniform bulk properties.
It’s a new and powerful idea that has yielded impressive results. The first big eye-opener was the demonstration of materials with a negative refractive index. Now additional counterintuitive concepts are in the pipeline, including “invisible” materials and mirrors that reflect light without shifting its phase.
Negative refractive index
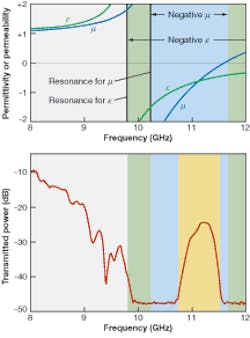
People working in optics normally think of refractive index n as a measure of the degree of refraction of a transparent material. However from a fundamental standpoint, refractive index is the square root of the electric permittivity ε and the magnetic permeability µ.
Normally both permittivity and permeability are positive in transparent materials, so refractive index is positive. One but not both of those properties can be negative in natural materials, making the refractive index imaginary, and thus strongly absorbing. Metals have negative permittivity at optical frequencies. Some materials have negative permeability at certain resonances, but they are not at optical wavelengths. In 1968, theorist Victor Veselago asked what would happen if both permittivity and permeability were negative in the same frequency range, and concluded that any such materials would have unusual optical properties including a negative refractive index.1
Veselago’s idea was largely ignored until about a decade ago when artificial materials were developed to respond in specific ways to electromagnetic waves. John Pendry of Imperial College (London, England) found that the magnetic fields in an electromagnetic wave could induce currents in coiled conductors, producing a magnetic effect with a resonant frequency that depends on the size and shape of the coil. In 1999, he demonstrated a metamaterial composed of arrays of coiled metal sheets, with resonances in the 15 to 20 MHz range used for magnetic-resonance imaging.2David R. Smith, now at Duke University (Durham, NC) first demonstrated negative refraction at microwave frequencies in 2001 using a metamaterial wedge consisting of an array of split-ring resonators deposited on printed-circuit boards (see Fig. 3). Refraction of the microwaves at an angle of -60° from the normal implied a refractive index of -2.7.4 Many initial reactions were sharply skeptical, but more detailed analysis supported the concept, and experiments confirmed that waves passing through negative-index metamaterials followed Snell’s law.
Superlenses for visible light
Shrinking metamaterial structures down to the sizes needed for visible or near-IR light took time, but last year they were made by several groups. Shuang Zhang of the University of New Mexico (Albuquerque) and colleagues made a metal-dielectric-metal multilayer metamaterial with negative index near 2 µm.5 Vladimir Shalaev and colleagues at Purdue University (West Lafayette, IN) used arrays of paired parallel gold nanorods to demonstrate a negative refractive index at 1.5 µm.6 Negative permeability was also demonstrated at visible wavelengths.7
A key attraction of negative-index optics is their potential to be “superlenses,” with resolution finer than the diffraction limit. Pendry pointed out that the peculiarities of negative-index focusing can bring together both normally propagating light and evanescent waves to create a nominally “perfect” image of an object on the opposite side of the lens.8 Superlenses made of thin metal foils, which have negative permittivity, were demonstrated last year by separate groups at the University of California at Berkeley and at the University of Canterbury (Christchurch, New Zealand).9, 10
In May, Gunnar Dolling of the University of Karlsruhe (Karlsruhe, Germany) and colleagues demonstrated another odd property of negative-index materials. Using femtosecond laser pulses near 1.5 µm, they measured both negative phase velocity and negative group velocity in a nanoscale metamaterial.11 Despite the two negative velocities, the Poynting vector was positive, so light pulses went through the metamaterial.
Invisibility, cloaking, and bizarre mirrors
Even stranger things are possible. A metamaterial with a planar layered structure of copper strips and dielectric substrates that looks like fish scales does not change the phase or intensity of polarized electromagnetic waves at certain frequencies, says Nikolay Zheludev of the University of Southampton (Southampton, England). This makes it functionally invisible in that narrow band, a property his group has demonstrated in the microwave region.12 The metamaterial is nearly transparent across a much wider range, but has high loss in a narrow band. If placed in front of a metal reflector, the structure reflects strongly across most of the spectrum. But in the narrow range where reflectivity is low, the metamaterial does not invert the phase of the reflected wave; more precisely, it inverts the direction of the magnetic field vector rather than direction of the electric field vector. At QELS in May, Zheludev reported demonstrating the same effect at optical wavelengths in an “optical magnetic mirror.”
Theoretician Graeme Milton of the University of Utah (Salt Lake City) and Nicolae Nicorovici of the University of Sydney (Australia) suggest another strange application of metamaterials-cloaking or hiding the presence of nearby objects. His idea is to create resonances that trap light. When nearby particles scatter light that resonates with the metamaterial, the trapped light would cancel it out, effectively hiding them from view. Cloaking could only work when objects were illuminated by coherent light, and so far has only been demonstrated on paper.13 But he says it offers science-fiction-like possibilities such as peeking inside a hollow object by putting one end at the edge of a cloaking field.
Alternative approaches to invisibility have been proposed independently by Pendry and by Ulf Leonhardt of the University of St. Andrews (St. Andrews, Scotland).14, 15 Their idea is to surround an object with a thick layer of metamaterial tailored to refract light around the object without ever touching it, so viewers would see no trace of it.
Outlook
Interest in metamaterials is growing rapidly, but the terminology remains hazy. As yet there is no hard and fast division between metamaterials and photonic crystals, a term so far used largely for microstructured materials composed of air, dielectrics, or sometimes semiconductors. The terminology will have to be pinned down as the field grows.
Challenges remain. Many of the most interesting effects so far have been demonstrated only on paper, and others have inherent limitations. Effects such as negative refractive index occur only near resonances, limiting them to use in narrow wavelength bands. Often the phenomena exist only over small scales. If cloaking works, it might hide only small objects in a room illuminated by a monochromatic laser; turn on an overhead white light, and the hidden objects would reappear. But it’s nonetheless a remarkable effect, and as with negative-index materials, we’ve only begun to explore the possibilities.
REFERENCES
1. V.G. Veselago, Soviet Physics Usp. 10 509 (1968).
2. J.B. Pendry et al, IEEE Trans. on Microwave Theory and Techniques 47, 2075 (1999).
3. D.R. Smith et al, Science 305, 788 (2004).
4. R. Shelby et al, Science 292, 77 (2001).
5. S. Zhang et al., Phys. Rev. Lett. 95, 137404 (2005).
6. V. Shalaev et al., Optics Lett. 30, 3356 (2005).
7. N. Grigorenko et al., Nature 438, 335 (2005).
8. J. Pendry, Physical Review Letters 85, 3966, (2000)
9. N. Fang et al., Science 308, 534 (2005).
10. D. Melville and R. Blaikie, Optics Exp. 13, 2127.
11. G. Dolling et al., Science 312, 892 (May 12, 2006).
12. V.A. Fedotov et al., Phys. Rev. E 72, 056613 (2005).
13. G.W. Milton and N.-A. P. Nicorovici Proc. Royal Society A: Mathematical, Physical and Engineering Sciences DOI: 10.1098/rspa.2006.1715.
14. J.B. Pendry et al, ScienceExpress, May 25, 2006 (doi: 10.1126/science.1125907).
15. Ul. Leonhardt, ScienceExpress, May 25, 2006 (doi: 10.1126/science.1126493)
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.


