WAVEGUIDES: Slabs with a gap efficiently guide terahertz waves

Waveguides will become important components of many terahertz optical systems. Conventional solid optical waveguides based upon total internal reflection (TIR), however, have losses that are too high. Because dry air exhibits low loss for terahertz radiation, hollow light pipes with highly reflective wall materials (for example, hollow photonic-crystal fibers) would seem ideal. But fabricating such light pipes with low transmission loss and low group-velocity dispersion has proved to be difficult.

Thin metal wires can guide terahertz waves with low loss and low group-velocity dispersion (see “Simulation matches experiment for wire waveguide”).¹ The effect is the same as the so-called Sommerfeld wave known to occur for microwave radiation propagating on metal wires of finite conductivity.² One disadvantage of Sommerfeld wires is the far-reaching radial extension of the electrical field; on the other hand, with their favorable propagation properties, these wires set a standard for terahertz waveguiding.

Now, a different sort of waveguide, a highly confining low-loss terahertz waveguide with low group-velocity dispersion, has been developed by researchers at Rheinisch-Westfälische Technische Hochschule (RWTH; Aachen, Germany). They investigated waveguiding along two parallel rectangular dielectric slabs with a narrow (subwavelength) air gap between them—called a split rectangular waveguide (SRW)—as well as along an air-filled dielectric tube waveguide (TW).

The guiding in both devices is provided by TIR, but with a high percentage of the optical power propagating within the loss-free gap or in the tube bore, respectively.³ According to Maxwell’s equation, the normal component of the displacement vector remains unchanged at the border between different dielectrics, meaning that the corresponding component of the electrical field strength increases steeply in air, which concentrates the optical power within that region.⁴

Guiding in the gap

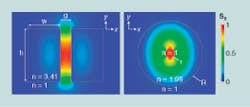
The researchers performed field simulations for guides of both geometries and mapped the distribution of the strength of the Poynting-vector z-component (see Fig. 1). For the SRW material they chose silicon, a dielectric in the terahertz spectral region with an index of refraction of 3.417 and a dissipation factor of 0.00001 at a frequency of 0.7 THz, and fused silica for the TW, which has an index of refraction of 1.95 and a dissipation factor of 0.001 at a frequency of 0.5 THz. In both structures, the Poynting vector z‑component reaches the highest values within the inner low-index regions. Varying the height of the SRW, but keeping a fixed ratio of height:width:gap of 1:1.6:5, the authors found 55% of the total power confined to the gap area when the height reached 90 µm, with only 25% guided within the high-index material. The corresponding simulations for the TW at a ratio of outer to inner radius of 2 resulted in a maximum of 26% for an outer radius of 175 µm.

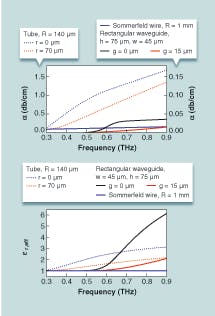
Attenuation and permittivity were calculated as a function of the gap and the inner radius for a frequency range from 0.3 to 0.9 THz, including a Sommerfeld wire as a reference (see Fig. 2). The SRW exhibited lower attenuation than the Sommerfeld wire (SW) and a much slower increase of the effective permittivity than for the bulk material. The slope of effective permittivity as a function of frequency—responsible for group-velocity dispersion—reveals that the SRW comes closest to the Sommerfeld wire in its properties.

FIGURE 2. Attenuation (top) and permittivity (bottom) as a function of frequency were calculated for split-rectangular and tube terahertz waveguides, with a Sommerfeld wire included for comparison. The left and right ordinates in the top figure differ by a factor of ten.

Another advantage of the SRW became apparent when bending losses were compared to those for the TW and Sommerfeld wire. In a result important for potential use in integrated optics, the cross section that encompasses 75% of the power in the SRW was determined to be 104 times smaller than for the Sommerfeld wire.

As yet, experiments have only been performed on a TW for which the attenuation and the effective permittivity in dependence on frequency were measured. Experimental data were in accordance with a dielectric dissipation factor of 0.2 and an effective permittivity of 4.5.

The investigation shows the considerable potential of split rectangular waveguides for integrated terahertz optics, as a result of their tiny structure, and of tube waveguides for endoscopic applications. “Using silicon micromachining techniques, we think that we will be able to fabricate and test SRWs very shortly and take full advantage of this approach,” says Michael Nagel, one of the Aachen researchers.