Subwavelength light spots are valuable for many forms of scientific experimentation; for high-resolution confocal and multiphoton microscopy, they are essential. Researchers at the Massachusetts Institute of Technology (MIT; Cambridge, MA) and Lightwave Instruments (Watertown, MA) are producing subwavelength light spots in a way that is based on an unusual approach to well-known theory.1 The approach, which shuns the use of conventional focusing optics and instead superposes many collimated laser beams on one another, relies only on flat mirrors and could thus be used for regions of the spectrum ranging from x-ray to long-wave IR.
Anyone delving into the mathematics behind Fourier optics will discover that a monochromatic wavefront of any shape can be mathematically decomposed into a (frequently infinite) number of plane waves of varying tilt, amplitude, and phase. This knowledge serves as a way to understand Fourier transforms. What the MIT and Lightwave researchers do, however, puts theory into practice. They attempt to create, as fully as possible, a group of plane waves that, when summed up, form a certain sort of converging wavefront.
Interfering beams create a spot
A single laser beam is split into many collimated beams, which are routed by mirrors so that they intersect all at once (piezoelectric actuators on some of the mirrors help maintain the relative phase of all the beams). Because high-angle beams create smaller spots, and because the number of beams is limited in practice, the researchers bring all the beams together in a high-angle cone, which simulates a single coherent beam that is focused by a high-numerical-aperture (NA) lens with a narrow annular (ring-shaped) aperture. Even though the individual beams are collimated, the combined result is a beam that focuses to a subwavelength spot.
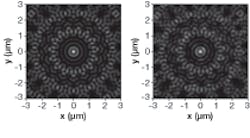
A collimated 488 nm argon-ion laser beam 0.5 mm in diameter was split into 15 beams. A system of flat mirrors matched the path lengths and phases of all 15 beams, combining them at a focal plane with an incoming half-angle of 72°, or an NA of 0.95. A 160×, 1.4 NA oil-immersed objective with a cover slip projected the resulting spot and surrounding area onto a CCD imager. Equal phases for all beams produced a 280-nm-diameter ring-shaped focus (zero-order Bessel-beam approximation), while setting the phases so that they incremented upward around the ring through a total of 2p produced a spot with a full-width-at-half-maximum (FWHM) diameter of 180 nm (first-order Bessel-beam approximation; see figure).
The Bessel beam is capable of forming only where all incoming beams intersect, placing an upper limit on its length. “In practice, however, we found that the length of the Bessel beam is limited by errors in the orientations of the wave vectors and the planarity of the wavefronts,” says Stanley Hong, one of the researchers. “We experimentally measured the length of the Bessel beam by translating the objective lens axially and observed that the Bessel beam disintegrates gradually over a length of about 100 µm. Over a length of 50 µm, the FWHM diameter of the focal spot increases from 180 to 210 nm.”
The power in the focal spot of the Bessel beam was on the order of 1 µW, which is admittedly very low, Hong notes. “Since the beams were collimated, most of the optical power ended up in the interference pattern outside the focal region,” he explains. “One straightforward way to increase the power in the focal spot would be to use focused (rather than collimated) beams.”
The researchers have theoretically explored the possibility of creating other shapes at the focus, though the results are unpublished. “In simulations, we’ve been able to create several propagation-invariant (or ‘nondiffracting’) patterns such as rings of various diameters and lateral line segments of various lengths,” says Hong.
Along with optical and x-ray microscopy, potential applications include maskless lithography and optical trapping.
REFERENCE
1. S.S. Hong et al., Applied Physics Lett. 88, 261107 (2006).
About the Author
John Wallace
Senior Technical Editor (1998-2022)
John Wallace was with Laser Focus World for nearly 25 years, retiring in late June 2022. He obtained a bachelor's degree in mechanical engineering and physics at Rutgers University and a master's in optical engineering at the University of Rochester. Before becoming an editor, John worked as an engineer at RCA, Exxon, Eastman Kodak, and GCA Corporation.
