Quantum computers might have revolutionized society by now, but there’s a snag: errors. Classical computers have errors, but they occur much less often and they’re relatively easy to correct. In stark contrast, quantum information is exceedingly fragile. And worse, errors come in two forms: bit flips and phase flips.
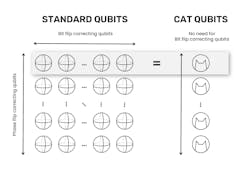
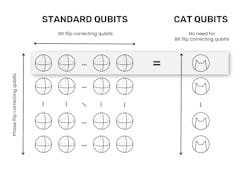
Only bit flips occur in classical computers and can be easily dealt with by redundancy, using many copies of each bit to take majority votes from time to time. Quantum errors can also be solved by repeating the information across several physical qubits. But if you need 30 physical qubits to deal with bit-flip errors and 30 for phase-flip errors, you end up with nearly 1000 physical qubits to make just one error-free logical qubit (see Fig. 1). That’s a typical figure for standard quantum architectures using transmons (superconducting charge qubit less sensitive to charge noise) and surface codes for error correction.
It makes for a hefty hardware overhead. And it only works if the fidelity of the physical qubits is good enough, which puts a huge burden on fidelity. So, this is the obstacle: an acute physical problem that error correction alone can at best turn into a massive engineering problem. What to do?
Photonics can light the way
Many physical platforms are currently competing to make quantum computing a reality. Indeed, many different quantum systems can play the role of the qubit, each with its own strengths and weaknesses. Think of trapped ions, neutral atoms, superconducting circuits, and even photons. Yes, light itself can be used to encode quantum information.
Optical photons bring together many advantages for quantum computing. They are easily produced and can be routed in optical fibers, propagating over long distances and remaining coherent for long times at room temperature, which means they don’t require expensive cryostats. Companies like Xanadu in Canada or Quandela in France have developed promising approaches to photonic quantum computing. All in all, it’s a great platform for scaling, but it’s much harder to run operations between qubits and program the quantum computer. This makes it more difficult to build all the necessary gate operations to achieve universality.
But it isn’t the only way optics can provide a key tool in the operation of a quantum computer. Other platforms rely heavily on optics to control and measure quantum systems. Lasers are used to read out the states of trapped ions, optical tweezers to manipulate the states of neutral atoms, and microwave photons to control superconducting circuits.
There are even state-of-the-art approaches to quantum computing where ideas from quantum optics provide more than just a tool—and provide a method that directly addresses the biggest problem in quantum information.
The cat qubit
The idea here is to attack the error problem head on: Schrödinger cat states are quantum superpositions of two coherent states of light that are effectively mirror images of one another.
The quantum logical “0” is a collective state of photons in which they all share the same amplitude and phase. It corresponds to the state of light created by a laser. The logical “1” is the same state except that the phase of each photon is the opposite. We take the same laser light as we did before, but delay it just as much as needed so that all photons have the opposite phase of the ones in our first beam.
Such states are often referred to as “classical” because they correspond to the usual excitations of resonators: using mirrors to trap the light of a laser in an optical cavity, the corresponding coherent state inside is described mathematically in the same way as a mass oscillating at the end of a spring.
The laws of quantum mechanics allow us to prepare not only these two distinct coherent states, but also superpositions of them. In the laser analogy, this would correspond to the laser emitting the same photons with two different phases at the same time. These states are called Schrödinger cat states, named after the famous thought experiment in which a cat could be both dead and alive due to quantum effects. Schrödinger’s aim was to show how absurd it would be if the principle of quantum superposition could be transposed to our classical world.
In the present case, no cats are harmed, but the idea is the same: we can generate and observe coherent quantum superpositions of classical states, not of cats, but of light. And the idea and first realization of these states originated in optics. Cat states of photons at microwave frequencies were then realized and French Physicist Serge Haroche was awarded a Nobel Prize in Physics in 2012 for this groundbreaking work in quantum optics.
Putting the cats to work
What’s the connection with the error problem? At Alice & Bob, we use superconducting circuits to generate, stabilize, and control qubits based on Schrödinger cat states (see Fig. 2). Cat states are interesting quantum objects that can teach us a lot about the fundamentals of quantum mechanics, but our goal is to create practical quantum computers. And it turns out cat qubits have one particular property that makes them eminently suitable for fault-tolerant quantum computing: a built-in ability to resist bit-flip errors.
For a cat qubit, a bit flip corresponds to flipping the phase of all the photons making up the coherent state. The more photons, or the stronger the laser intensity in the previous analogy, the more difficult it is for the environment to flip these phases. In fact, bit-flip suppression rises exponentially with the number of photons contained in the coherent state. In a recent experiment, we demonstrated a six order of magnitude increase in the bit-flip time of our cat qubit, from a few microseconds to more than 10 seconds!1
This means a quantum computer based on cat qubits wouldn’t have to worry about bit-flip errors. It remains only to correct for one kind of error: phase flips. Our error correction code is therefore greatly simplified, and we expect to build logical qubits out of cat qubits much earlier, resulting in fault-tolerant quantum computers using 60 times fewer resources than the current state of the art, as demonstrated in a recent simulation of the overhead required to carry out Shor’s famous algorithm to factorize large numbers.2
Taming Schrödinger’s cats
The cat qubits we engineer at Alice & Bob are made of photons, but not the ones you can see. They’re in the microwave range, with wavelengths about 100,000 times longer than visible photons and close to telecom frequencies. These photons are not produced by lasers, but rather by microwave sources. And they don’t propagate in optical fibers, but in coaxial cables. Instead of measuring them with photodiodes, we digitize their electromagnetic waves.
Temperature is even more important. If we tried to encode quantum information in the state of a few microwave photons in a quantum memory at room temperature, it would be overwhelmed by the hundreds of thermal photons generated in the equipment itself. To avoid this problem, our memories are cooled down to 10 millikelvin, close to absolute zero, in specially designed cryostats (see Fig. 3), where the average number of thermal photons is approximately zero.
There are various ways to make a quantum memory that can trap microwave photons. They all rely on superconducting materials, which can conduct electrical current without loss, which is another reason to lower the temperature.
So how do we do this? Like most quantum states, cat states are fragile and require stabilization. Once prepared in a quantum memory, they would inexorably collapse into the vacuum by gradual loss of photons. But this collapse can be prevented by forcing the memory to gain and lose photons in pairs rather than one by one—a process called two-photon dissipation. We engineer this unusual property by coupling a second electromagnetic mode to the memory. Unlike the memory, this “buffer” is designed to lose its photons very quickly within this environment. We then implement a 2-to-1 photon exchange process between the memory and the buffer.
When the buffer frequency is half the memory frequency, this process is equivalent to second harmonic generation, or frequency doubling, well known in optics. The difference is that we can do it off-resonantly using a pump. We end up in a situation where pairs of memory photons are converted into buffer photons and then quickly lost. Going the other way, a drive on the buffer is converted into a two-photon drive on the memory, which makes the cat states stable.
Building quantum computers
Of course, if we want to process quantum information, we must apply logical operations, or gates, to our qubits. Single-qubit gates are obtained by driving the cat with a single-photon drive from a microwave source which is the equivalent of a microwave-frequency laser. The two-qubit gate needed to perform quantum error correction is the controlled-NOT (CNOT) gate. This flips the state of a target cat precisely when the state of a control qubit allows it.
To implement the CNOT gate, we engineer another well-known optical effect: an optomechanical interaction. In optomechanical systems, the radiation pressure of photons contained within an optical cavity displaces a mirror attached to a spring, thereby forming a resonator. This interaction is not native to superconducting circuits but, like the two-photon dissipation, is engineered using parametric processes.
This account demonstrates that the crucial features of cat qubit technology rely on our ability to perform nonlinear optical operations. How is this done for microwave photons? In fact, we use Josephson junctions, nanoscale elements made of a layer of insulator sandwiched between two superconductors. By building superconducting circuits containing Josephson junctions, we can design the desired interactions between the components of our system.
This is rather like what happens in nonlinear optics when a nonlinear crystal is inserted in an optical cavity. But an important difference with optics is that the interaction between microwave photons and Josephson junctions can be made more than a hundred times stronger than the typical interaction between optical photons and crystals. This means the nonlinear effects engineered in superconducting circuits are likewise stronger.
Only a few years ago, it looked like building an error-protected quantum computer might be an impossible feat. It’s certainly one of today’s major technological challenges, but we’re getting closer to it every day at an increasing rate—thanks to technologies like cat qubits, which benefit greatly from the field of photonics.
REFERENCES
1. U. Réglade et al., arXiv:2307.06617v1 [quant-ph] (Jul. 13, 2023); https://arxiv.org/pdf/2307.06617.pdf.
2. E. Gouzien et al., arXiv:2302.06639v2 [quant-ph] (Aug. 4, 2023); https://arxiv.org/pdf/2302.06639.pdf.
About the Author
Nathanaël Cottet
Senior Experimental Physicist, Alice & Bob
Nathanaël Cottet is senior experimental physicist at Alice & Bob (Paris, France).