After 40 years, a team of researchers has finally proven the elusive Anderson localization phenomenon really does exist for electromagnetic waves by using advanced computational electromagnetics to show that optical waves can be trapped within three-dimensional (3D) randomly packed micro- or nanoparticles (see video).
Back in 1977, Philip W. Anderson was awarded a Nobel Prize in Physics for his work in 1958 with two others for their “fundamental theoretical investigations of the electronic structure of magnetic and disordered systems.”
Electron waves inside a material either move freely or get trapped due to scattering and interference—depending on the amount of randomly distributed defects within the material. Anderson’s seminal work was the first to predict metals can act as insulators when disordered.
But conclusively proving that electromagnetic waves in 3D propagating at the speed of light with different polarizations can also become trapped or localized had to wait for advanced computing technologies to simulate the large scattering systems necessary to prove this phenomenon exists for light.
The team of researchers from Yale University, the French National Center for Scientific Research (CNRS), Missouri University of Science and Technology, and the University of Wisconsin–Madison worked with Flexcompute, a simulation technology startup, using their computational process to increase the speed and scale of numerical simulations to successfully observe Anderson localization.
On May 27, 2021 at 11:13 p.m., Alexey Yamilov, a physics professor at Missouri University of Science and Technology, sent everyone else on the team an email with the subject line: “Houston, Tranquility Base here. The Eagle has landed.” Translation for anyone not old enough to get the cool nod to the moon landing: they’d just confirmed Anderson localization of light for the first time.
“Anderson localization of light has been studied for more than 40 years,” says Hui Cao, a professor of applied physics at Yale University. “There’s been a lot of interest—both experimental and theoretical—but, until now, no conclusion was ever reached about whether or not it was possible. I’ve been intrigued by this a long time, and my colleagues have also worked on it a long time. It was just incredible to finally see it, because we’ve been studying it for so long.”
This discovery opens “a wide range of avenues in both fundamental research and practical applications using 3D localized light,” she adds.
What exactly is Anderson localization?
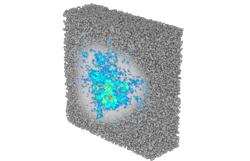
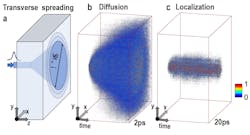
Anderson localization is essentially the halt of diffusive wave propagation within disordered systems (see Fig. 1). Wave interference complexity makes it extra difficult for researchers to observe the phenomenon.
“Light propagates along a straight line in a ray, but if you put obstacles in its way, it scatters from one obstacle to another and performs a kind of walk,” explains Sergey Skipetrov, a research scientist at CNRS. “At the end, if you put many of these obstacles around it randomly, this random walk behaves very much like a bouncing ball. This model of random walk is used to describe light propagation within biological tissues, for example.”
But corrections to this random walk can trick you because light has a phase—it’s a wave—and it can interfere. “We can measure this correction and, if the disorder is strong enough, if there are many strong obstacles, this interference effect can block propagation and the random walk picture will break down,” says Skipetrov. “This is Anderson localization.”
This phenomenon is very general and can occur for light, sound, or any other type of wave. “For a very long time, people thought Anderson localization behaved the same for every type of wave,” Skipetrov adds. “Nobody really paid attention to the fact that light is a vector wave. It means you have an electric field and a magnetic field, which are vectors pointing somewhere. But these vectors weren’t considered very important for these disordered problems because, in particular, of the random scattering involved that makes all of the polarizations random.”
It turns out these active fields, such as the electric field, can be not only perpendicular to the direction of propagation (transference waves), but also parallel (longitudinal waves). (See Fig. 2.) “But this can only happen if the medium is disordered,” says Skipetrov. “You need some variation in the dielectric constant for this to occur. And it’s also precisely what you need for Anderson localization.”
By introducing this randomness into the dielectric constant via obstacles or particles, you approach Anderson localization and also change the nature of the wave, which is purely transversal in free space, but becomes partially longitudinal within a disordered medium.
And by doing so, the researchers made a key discovery: this longitudinal wave breaks down Anderson localization within a dielectric medium such as silicon or glass.
“In a dielectric medium, we show there’s no Anderson localization—in contrast to what people previously believed,” says Skipetrov. “This allows us to propose a system in which we can observe Anderson localization by getting rid of the longitudinal wave. In our work, we do it by considering conducting particles—perfectly reflecting particles where the wave doesn’t penetrate inside the particle.”
Put another way: the wave is deflected by the particles so it doesn’t penetrate inside the particle, and the space where the wave exists is a free space between the particles. “It’s just empty space,” Skipetrov says. “And a longitudinal wave can’t exist within this free space, so everything else works as it does for other types of waves like sound or electrons within disordered solids.”
Running the simulations
During Anderson’s Nobel Prize lecture in 1977, he mentioned that since Anderson localization is such a confusing phenomenon, “you’d need to “resort to the indignity of numerical simulations” to prove its existence.
How confusing is it? “Anderson localization is an emerging phenomenon,” says Yamilov. “You can’t predict it based on the properties of a single scatterer or particle. It emerges from interactions of the waves with many, many particles.”
Yamilov likens the phenomenon to trying to predict how society will behave from knowing how a single person behaves—almost impossible to do. “People interact and what is revealed is that common behavior is an emerging behavior that comes from many, many constituents,” he says. “In our case, multiple waves interfering creates something new. So, we needed a very large system where all of these interactions are accounted for.”
Flexcompute’s simulations expand the speed (by 100 to 1000X in some cases) and scale of simulations by using novel hardware. And their FDTD software Tidy3D accelerates numerical solutions by orders of magnitude.
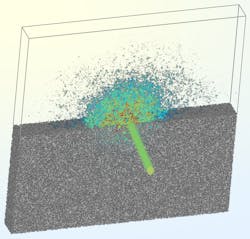
It enabled the team’s large-scale microscopic simulations of electromagnetic wave propagation in 3D (see Fig. 3), which is the first report of wave localization within random groups of metallic particles at a large scale.
“Our server doesn’t run on a regular computer, it runs on ones we had made to work for this problem as efficiently as possible,” says Momchil Minkov, senior scientist at Flexcompute. “We selected the best hardware and wrote the software for the hardware and problem—taking everything into account: the physics, the mathematics, and computational power—to speed it up as much as possible and open up the scale for these large problems.”
How fast is it? “When we tried to do a large simulation in the past, it could take days,” says Cao. “This took 30 minutes at most, which allowed us to try many different random configurations, different system sizes, and different structural parameters to see whether we could get 3D localization of light.”
Tapping into Anderson localization
The team made several important discoveries for future work. First, it’s impossible to localize light within 3D random dielectric aggregates. Second, they demonstrated evidence of Anderson localization of electromagnetic waves within random packings of metallic spheres.
Beyond resolving these long-standing questions, their work opens the door to solving many other problems such as optimizing complex optical signals within data centers or developing nanostructured lenses for chip-based LiDAR.
“3D confinement of light in porous metals can enhance optical nonlinearities, light-matter interactions, and control random lasing and targeted energy deposition,” Cao says. “Flexcompute’s advances in software and computation will let us solve a lot of other important problems we’ve been working on for a long time.”
FURTHER READING
A. Yamilov et al., Nat. Phys. (2023); https://doi.org/10.1038/s41567-023-02091-7.
