Optical Magnetism: Photons induce high levels of magnetism in optical materials
Researchers at the MURI Center for Dynamic Magneto-Optics (DYNAMO) at the University of Michigan (Ann Arbor, MI) have both observed and explained the presence of photon-induced magnetic dipole (MD) scattering (optical magnetism) in certain crystalline materials that is just as intense as ordinary Rayleigh scattering.1,2
The experiments show for the first time that induced magnetic dipole scattering can equal electric dipole scattering through a two-photon magneto-electric interaction that makes "enhanced optical magnetism" possible and offers an alternative to metamaterials or multiferroics (ferroelectric, ferromagnetic, or ferroelastic) for the purpose of controlling magnetic properties of materials with light (see Fig. 1). The research is the first observation and explanation of a photon-induced, magneto-electric interaction at the molecular level and was aided by collaborators at Riken in Japan, Northwestern University, Stanford University, and the University of Central Florida.
Part I: Radiant optical magnetization experiments
Although never thought possible in previous measurements of electric and magnetic dipole light scattering at low intensities, optical magnetism does occur at (nonrelativistic) intensities exceeding approximately 108 W/cm2. This is possible because a single photon is capable of imparting orbital angular momentum to a garnet or quartz crystal (at the molecular level) that may subsequently be converted to rotational angular momentum through the action of magnetic torque from a second photon.
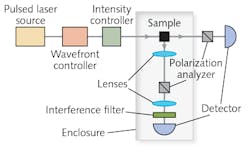
In the experiments, two pulsed laser systems (one at a 775 nm wavelength emitting 150 fs pulses at a 1 kHz pulse rate; the other at an 800 nm wavelength emitting 20 fs pulses at 80 MHz) provided input light to garnet and quartz materials-the resulting light-scattering signals and their radiation patterns (polar power plots) were recorded (see Fig. 2). A wavefront controller provided automatic dispersion compensation, and a filter excluded vibrational Raman scattering and impurity fluorescence. Scans were completed at various intensity levels and at various polarization orientations. The measured patterns were decomposed into polarized and unpolarized components, resulting in four datasets for each material, with vertical and horizontal electric dipole (ED) and magnetic dipole (MD) components.
Within the intensity range for the experiments, no ellipse rotation or cross-polarized four-wave mixing was observed, meaning that the scattering that was polarized perpendicularly to the Rayleigh scattering could only take place through second-order magnetization at the molecular level—namely, via a magneto-electric interaction. Competing interactions, such as second-order, all-electric interactions and other polarization-rotating interactions, were carefully eliminated by selecting nonchiral, isotropic samples.
The MD scattering was found to differ in intensity in quartz and garnet materials at a fixed input power. However, the exchange of angular momentum between orbital and rotational (librational) motion through the action of magnetic torque was deemed to be responsible in both materials for resonant magnetic transitions at the optical frequency.
The finding that magnetic scattering intensity can equal the intensity of Rayleigh scattering is very unexpected, and has apparently gone undiscovered until now because of a plethora of all-electric nonlinear processes that tend to obscure the results. Also, complete radiation patterns were never recorded in previous scattering experiments at sufficiently high intensities.
Part II: Theory of induced optical magnetism
Enhancement of magneto-electric interactions can take place when an initial photon establishes an electrical polarization within a material and imparts orbital angular momentum to its constituents. This happens on all allowed electric dipole transitions between L=0 and L=1 molecular states. Subsequently, a second photon can exert magnetic torque on the orbital angular momentum of a molecular excited state, causing an exchange of orbital and rotational angular momentum.
Through conversion of orbital motion of the optical excitation to rotational motion of the molecule, the second step of this magneto-electric interaction de-excites the molecule and effectively increases the radius of charge motion, thereby enhancing the magnetic dipole of the process (since that depends on the area enclosed by the current within the molecule). This finding has significant implications for materials that were once thought to be "nonmagnetic." Indeed, this type of induced magnetism should take place in all dielectric media and could enable new types of optical switches, energy conversion processes, or the generation of magnetic fields without requiring current-carrying coils.
The researchers showed analytically how the magnetism is optically induced within their samples. Basically, the process initiates charge motion with the electric force of light and deflects it with the Lorentz force to form molecular current loops. The big surprise is that torque exerted by the magnetic field component makes the overall (two-photon) process nearly resonant.
Minh Tuan Trinh, a postdoctoral researcher at the DYNAMO Center, says, "The second step in the magneto-electric interaction is analogous to the Einstein-de Haas effect, wherein the kinetic energy of spin angular momentum in an unmagnetized iron bar can be converted to macroscopic rotary motion of the bar by application of an oscillatory magnetic field. In the experiments at DYNAMO, it is orbital angular momentum rather than spin that is converted to rotary motion of molecules through a similar torque interaction involving the optical magnetic field."
REFERENCES
1. A. A. Fisher et al., Opt. Express, 24, 23, 26055-26063 (Nov. 14, 2016).
2. A. A. Fisher et al., Opt. Express, 24, 23, 26064-26079 (Nov. 14, 2016).
About the Author

Gail Overton
Senior Editor (2004-2020)
Gail has more than 30 years of engineering, marketing, product management, and editorial experience in the photonics and optical communications industry. Before joining the staff at Laser Focus World in 2004, she held many product management and product marketing roles in the fiber-optics industry, most notably at Hughes (El Segundo, CA), GTE Labs (Waltham, MA), Corning (Corning, NY), Photon Kinetics (Beaverton, OR), and Newport Corporation (Irvine, CA). During her marketing career, Gail published articles in WDM Solutions and Sensors magazine and traveled internationally to conduct product and sales training. Gail received her BS degree in physics, with an emphasis in optics, from San Diego State University in San Diego, CA in May 1986.