High-energy Lasers: Extreme light in zeptoseconds
TOSHIKI TAJIMA, GÉRARD MOUROU, and JONATHAN WHEELER
Traditionally, pulse compression is concerned with low-energy laser pulses. Recently, however, the possibility to compress petawatt and even higher-energy pulses with tens of joules of energy was demonstrated. The interaction of these pulses with a relativistic plasma mirror results in further compression to the sub-attosecond time regime, opening a route to multi-exawatt pulses in the single-cycled x-ray regime.
These high-energy pulse compression techniques will open a floodgate of novel applications such as compact and efficient laser ion accelerators, on-chip tera-electron-volt particle accelerators, and light materialization in a vacuum. In addition, pulses with attosecond-zeptosecond duration are naturally in the x-ray regime (1–10 keV) and enable study of fundamental physics at tera-electron-volt energies and beyond, cosmic acceleration, vacuum nonlinearities, light-mass weak coupling fields such as dark matter and dark energy, radiation physics in the vicinity of the Schwinger field, and zeptosecond dynamical spectroscopy in a vacuum, as well as affordable proton sources for proton therapy.
Shorter pulses, higher energy
Leveraging years of research on high-energy lasers, we realized that the route to reach peak power beyond 10 PW was not to increase pulse energy—an increasingly costly endeavor—but rather to decrease the pulse duration to the attosecond-zeptosecond time scale.1 In this way, exawatt power can be reached with a simple joule of energy.
With the discovery of chirped pulse amplification (CPA) and later optical parametric CPA (OPCPA), we have seen a considerable jump in laser pulse peak power by 6–8 orders of magnitude, peaking from 1015 to 1022 W/cm2 or 4 orders of magnitude above the level where the electron quiver energy equals the rest mass energy (or 1018 W/cm2 of the electron). This heralds the relativistic laser plasma interaction and the subatomic regime, including nuclear and particle physics.2,3
The next intensity level leads to a quiver energy equal to the proton rest mass, or 1025 W/cm2. It is these enormous intensities that the large-scale European laser infrastructures such as the Extreme Light Infrastructure (ELI), LMJ, and Apollon, as well as others in Russia, China, and Korea, vie to deliver. However, to enter the nonlinear quantum dynamic domain, we must go much higher with intensities in the 1029 W/cm2 range.
Light-vacuum materialization
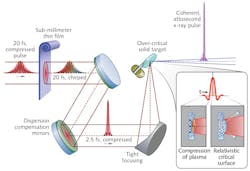
The strategy that we have adopted in collaboration with ELI-NP (http://www.eli-np.ro) for the efficient production of high-energy subattosecond pulses with energies >1025 W/cm2 is simple, low cost, and uses existing petawatt or petawatt-to-be facilities. The compression technique is performed in two steps: first compressing a typical 20 fs, 20 J near-infrared (NIR) pulse into a single cycle while maintaining upwards of 15 J of energy, and secondly, using a relativistic plasma mirror to drastically compress the pulse from 2.5 fs to the attosecond-zeptosecond (10-21 s) regime.
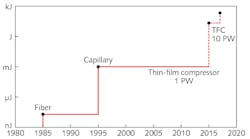
Current compression techniques rely on a fused silica fiber or hollow-core capillary, filled with noble gases to produce the necessary spectral broadening.4-6 However, they can only accommodate pulses with low energy from the nano- to millijoule level, with the transition from one technique to the other leading to a sharp increase in the compressible energy (see Fig. 1).To increase pulse energy even more, bulk compression was attempted by Corkum and Rolland.7 However, the material nonlinearity is strongly influenced by the Gaussian intensity profile of the beam and makes the pulse impossible to compress uniformly except for the central area near its peak intensity—a non-uniformity that has greatly diminished the attractiveness of bulk compression.
To solve the uniformity problem, we suggest the use of modern petawatt lasers that exhibit pulses with top-hat profiles in amplitude and phase in thin (sub-millimeter) bulk films to produce single-cycle pulses in the tens-of-joules power level (see Fig. 2). The thin-film compression (TFC) technique relies on inexpensive sheets of plastic, or alternatively, sub-millimeter glass plates of uniform thickness—but not necessarily flat—placed within the petawatt pulse beam transport to produce near-constant self-phase-modulation (SPM) across the beam while minimizing energy losses. The large-aperture material must be capable of withstanding high-intensity laser shots without breaking, while being easily replaceable.Numerical simulations carried out assuming a plastic film interacting with a laser similar to that recently commissioned at the CETAL PW petawatt laser facility (http://cetal.inflpr.ro) based at the Institut National de Laser, Plasma et Radiophysique (INFLPR; Magurele, Romania) showed that pulses of 27 J of energy within 27 fs at a wavelength of 800 nm are compressible to a 3 fs (single-cycle at 800 nm) pulse by using two thin-film stages.8
The efficiency of the proposed scheme allows for the multiple compressor stages to produce the desired compression while maintaining the B integral in each stage limited to around 3. Note that tightly focusing this single cycle forms an ellipsoid in space with λ3 dimensions.
To further compress the NIR single-cycle pulse to the atto-zepto regime, we will use a laser-driven reflective surface that moves in and out under the influence of the very strong incident pulse. At this point the intensity can be in the 1023 W/cm2 region associated with a formidable light pressure and can move the critical surface at relativistic speeds. In this λ3 relativistic regime, Naumova et al. predicts a reflected pulse duration T—compressed by the relativistic motion of the mirror toward the pulse—scaling as:
T = 600 (attosecond)/a0
Here, a0 is the normalized vector potential of the laser pulse, which is unity at 1018 W/cm2 and scales as the square root of the intensity.9 At 1023 W/cm2, a0 is approximately 500 and a 1 attosecond pulse can be produced. It is remarkable to note that 1 J of reflected energy delivered by an attosecond pulse is sufficient to reach exawatt power levels.
High-energy electron and ion acceleration
High-frequency photons have an advantage for driving wakefields in high-density matter. The current mainframe approach to increase laser wakefield acceleration (LWFA) energy gain is to make the plasma density lower for a fixed optical laser frequency. This is based on well-known laser wakefield scaling techniques.10
In LWFA, the energy gain is limited by the critical density of the plasma, with the high-intensity LWFA energy gain given by:
εe= a02 mc2(nc/ne)
where ne is the electron density. The critical density of a plasma, nc, is defined by the laser frequency and increases with increasing photon frequency or energy. For 1 eV optical photons, nc is about 1021/cm3, while for x-ray photons of 10 keV, nc is about 1029/cm3 and is well above solid densities.
Our new path toward higher energy gain (and yet smaller, more compact accelerators) is to increase the photon energies to the level of x-rays by keeping the ratio nc/ne large without making ne lower. Therefore, going to a higher photon energy allows for a greater achievable energy gain in that an important benefit of a higher-density plasma is its ability to support a larger acceleration gradient.
Shifting to extreme x-ray-driven wakefield acceleration dramatically allows acceleration to larger energies to be achieved over shorter distances, even suggesting tera-electron-volt energies over centimeter distances (that is, tera-electron-volts on a chip)—103 times the previous results achieved for optical lasers in gases and 106 times that of current radio frequency technology.
To date, these energy levels have only been achieved at CERN (Geneva, Switzerland) and require kilometers rather than a few centimeters using a laser facility such as the petawatt facilities currently being built.
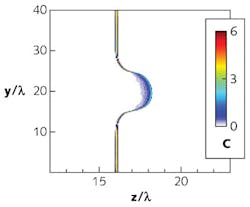
Our choice of materials in the high-density regime is now nanomaterials with nanoholes.11 In addition, the current compression of optical lasers to a single cycle (even before compression into the x-ray laser) have such inherent applications as drivers of ion acceleration (see Fig. 3). Effective, compact, and coherent acceleration of ions by the ponderomotive force of a single-cycled laser pulse results in high-quality, 1 GeV pulses by avoiding instabilities that arise in other laser-driven methods. A large factor of energy gain is seen in this laser piston regime.12In summary, today's high-peak-power lasers producing petawatt pulses with top-hat profiles, combined with thin-film/plate compressors, have the capability to produce 100 PW pulses with 2.5 fs single cycles. Focused to a spot size limited by the laser wavelength, it is predicted that their interaction with solids will generate attosecond or even zeptosecond multi-exawatt pulses in the x-ray regime, with the acumen to drive giant acceleration in crystals to the tera-electron-volt per-centimeter regime.
This achievement will not only provide the aforementioned all-optical understanding of high-energy physics phenomena, but will underpin new compact sources of protons, neutrons, and muons with more applications in fundamental physics, and for societal applications like compact proton therapy or nuclear waste transmutation.
REFERENCES
1. G. Mourou et al., Eur. Phys. J. Spec. Top., 223, 1181 (2014).
2. D. Strickland and G. Mourou, Opt. Commun., 56, 219–221 (1985).
3. A. Dubietis et al., Opt. Commun., 88, 437–440 (1992).
4. D. Grischkowsky, Appl. Phys. Lett., 41, 1, 1–3 (1982).
5. R. L. Fork et al., Opt. Lett., 12, 7, 483–485 (1987).
6. M. Nisoli et al., Appl. Phys. Lett., 68, 20, 2793–2795 (1996).
7. C. Rolland and P. B. Corkum, J. Opt. Soc. Am. B, 5, 3, 641–647 (1988).
8. M. Guillaume et al., CLEO 2013 paper CTh5C.5 (2013).
9. N. M. Naumova et al., Phys. Rev. Lett., 92, 063902 (2004).
10. T. Tajima and J. M. Dawson, Phys. Rev. Lett., 43, 4, 267–269 (1979).
11. T. Tajima, Eur. Phys. J. Spec. Top., 223, 1037 (2014).
12. T. Esirkepov et al., Phys. Rev. Lett., 92, 175003 (2004).
Toshiki Tajima is Rostoker Chair professor in the department of Physics and Astronomy at the University of California at Irvine, while Gérard Mourou is professor and director and Jonathan Wheeler is researcher at DER-IZEST, École Polytechnique, Palaiseau, France; e-mail: [email protected]; www.izest.polytechnique.edu.