Lasers light the way toward quantum computing
While the idea of using quantum mechanics principles such as superposition and entanglement to perform computations is at least several decades old, it’s only within the past few years that the technology to implement practical quantum computers became available. High-purity, low-noise laser sources are among the key enabling technologies for emerging quantum computing architectures. Advanced laser systems will play a pivotal role as quantum hardware disrupts the field of computer science.
The interest in building laser systems suitable for quantum computation is tied to the inherent benefits of quantum computing itself. Just as bits are the fundamental building blocks of modern digital computers, two-level systems called qubits form the foundation of quantum computers. A qubit can exist in coherent superposition of two binary states (zero and one), so it can be used to perform certain calculations much more rapidly than conventional computers.
Many practical problems in physics, chemistry, and biology, as well as problems in such diverse fields as accounting1 and automotive design,2 could benefit from quantum computing techniques. These and other fields face problems currently requiring exponential execution times, which could take decades to solve on even the fastest conventional supercomputer. Such computations could be performed much faster (in polynomial time) on a suitable quantum computer. These range from simulations of the world around us to optimization and sorting problems, factoring large prime numbers (the basis for modern encryption techniques that support a trillion-dollar global electronic commerce system), and improving existing algorithms such as artificial intelligence and machine learning. While quantum computers won’t replace conventional systems anytime soon, there are enough high-value problems within this category to drive multi-million-dollar investments in the development of practical quantum computers.
It’s useful to think about quantum computing as being in the earliest stages of its development, much like conventional computers. Indeed, before Charles Babbage and Ada Lovelace developed the first modern computer or difference engine to calculate logarithms, performing such computations was done by skilled humans whose job title was “computer” (just as someone who works with paint was called a painter).
There are many historical examples of such “computers,” including Katherine Johnson, Dorothy Vaughan, and Mary Jackson who played a vital role in the early days of the U.S. space program.3 Babbage’s difference engine used mechanical gears to execute programs developed by Lovelace using punched holes in paper tape—arguably the first implementation of bits in a mechanical computer. Subsequent computer architectures found new ways to represent bits, including voltage and current fluctuations in vacuum tubes, polarized photons, and electron states within silicon chips.
Implementing qubits
There are also many ways to implement qubits, and it’s likely we haven’t yet found the optimal way to achieve this in a quantum computer. For example, commercially available systems such as the IBM Q System and similar hardware from Google and Intel rely on superconducting wires cooled to near-absolute zero to realize qubits. The success of these systems has led researchers to investigate alternative quantum computing architectures that could operate under less extreme environmental conditions. Laser systems with specific properties are critical to many of these recent efforts because of the role it plays in multilevel physical systems.
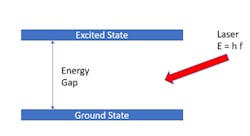
A qubit is a two-level system, in which two states can exist in a stable superposition. For example, consider two internal energy states within an atom—a ground state and an excited state (see Fig. 1). There is a discrete energy gap separating these states, and they can be coupled together using laser radiation at a specific frequency (where the laser energy and frequency are related by Planck’s constant, h). The atom’s state evolves in a well-defined phase relationship with the laser radiation (in other words, coupling between the laser and the atom is coherent). By applying laser pulses with a controlled frequency and duration, it’s possible to create a superposition state between the two atomic energy levels, effectively controlling the probability of finding the atom in the excited state or the ground state.
This process shows whether an atom is in the ground state, excited state, or both simultaneously (analogous to the famous Schrodinger’s Cat experiment). When measuring the qubit, it collapses into either the excited or ground state with some probability and can be reverted to a conventional zero or 1 value. By combining multiple two-level systems, it’s possible to create entangled states, in which the value of one qubit affects the value of another. Precisely tuned laser pulses that control the coherent interaction are used to construct quantum logic gates, just as conventional computers use Boolean logic gates to process bits.
In a quantum computer, a sequence of quantum gates operating on one or more qubits is used to implement quantum algorithms. We can measure the probability that a quantum gate is working as designed (or more generally, the probability of achieving a target quantum state) as the fidelity of a quantum logic gate. Fidelity is essentially the probability that entanglement between two states has been successful. If the fidelity drops below a threshold level, gate errors will occur and the quantum calculations will be corrupted. Quantum gate fidelity is limited by how well we can control the parameters of laser pulses used to interact with qubits. This means very high-purity, low-noise optical sources are fundamental to the construction of practical, scalable quantum computers.
One type of qubit based on single trapped atoms are known as optical qubits. In a design known as an ion trap, the atomic energy levels are chosen such that the excited state lasts for as long as possible (on the order of a second or two using current systems). There are significant research challenges to overcome when realizing practical optical qubits. One of the most significant is laser linewidth, which sets an upper limit on the coherence time for interactions between the laser source and the qubit. To take advantage of properties such as superposition, a quantum computer must perform all its calculations before the system loses coherence. This is analogous to using the calculator function on your cell phone when the battery is running out; you only have a limited time to complete your work before the phone dies and your calculation is forced to stop.
It’s desirable to maximize coherence time in a quantum system to enable performance of more lengthy calculations. Achieving a long-excited state lifetime requires laser sources with extremely narrow emission linewidths, on the order of perhaps 1 Hz.4 This is well below the range of many standard laser systems, which operate with linewidths between a few hundred kilohertz to several megahertz. Significant linewidth reduction and stabilization is required for high finesse laser cavities, which are insensitive to even small vibrations and other noise sources.
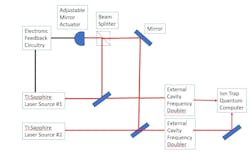
Advanced linewidth reduction systems have been developed using Ti:sapphire lasers at 729 nm center wavelength, with a 1 Hz linewidth and feedback stabilization from a high finesse external optical cavity. This makes it possible to create high-fidelity entangled qubit logic gates (see Fig. 2). More specifically, ion traps can be constructed using a steel vacuum chamber cooled to nearly -450°F. A dozen lasers at slightly different frequencies are directed into this chamber ionizing a combination of calcium and strontium atoms, which are held in an electric field and brought together to form a crystal.5The frequencies required for laser cooling calcium and strontium ions, entangling them, and reading out the results all fall within the same portion of the optical spectrum, which simplifies the laser system requirements. This material system can also be manipulated by infrared light, for which there are a wide range of available laser sources, as opposed to other materials that require ultraviolet frequencies to excite and trap ions. While device specifications vary, output power on the order of hundreds of milliwatts to a watt or more should be possible in the short-term using these devices. Strontium and calcium energy states can become entangled, so that reading the state of one qubit (for example, by interrogating the crystal with a laser wavelength that will only interact with the calcium ion) will also yield the state of the strontium qubit. A fidelity of 94% has been measured in the calcium/strontium crystal, sufficient to prove this concept is viable for quantum computations; variations on this structure have achieved fidelity of nearly 99%, among the highest gate fidelities yet reported.
An alternative approach known as hyperfine qubits encodes information in two sub-levels of the ground state of alkali-earth materials. Two laser frequencies separated by a few gigahertz (the energy gap of the qubit) provide coherent coupling through stimulated Raman transitions. In this case, the ability to control coherence isn’t determined by the linewidth of each laser, but rather the relative phase noise between the two sources. Typically, these two sources can be implemented by phase locking two lasers to maintain a precise frequency offset. It’s also possible to use electro-optic modulation to produce two frequencies through sideband generation. Raman transitions are non-resonant, meaning relatively high optical power is required to achieve high-fidelity logic gates. Such a system requires both low phase noise and high power, typically at ultraviolet wavelengths.
One recent implementation for calcium ion hyperfine qubits uses two phase-locked and frequency-doubled Ti:sapphire lasers, operating at 397 nm wavelength with a frequency offset of 3.2 GHz. The combined system can deliver over 3 W of total power. This approach is suitable for high-fidelity quantum gates, because it features low phase noise (7 mrad rms between 10 kHz and 1 MHz).
Technical challenges
Many technical challenges remain, including scaling these systems to large enough numbers of qubits for practical calculations. Systems such as those described earlier have only been demonstrated for a few qubits at a time; hundreds or thousands of qubits are desirable for many applications. This will require greatly increasing laser output power—on the order of several watts to tens of watts or higher—while maintaining low noise and fine line widths. Precision alignment of optical components in future systems may also benefit from advances in integrated optics and modulators.
Further, there are proposed implementations of qubits that do not use ion traps, but instead encode qubits into two optical modes of a single photon (such as light polarization).6 In principle, photonic qubit systems would not need to be cooled near absolute zero to function and could facilitate transmission of qubits over long distances using fiber-optic cable, provided the cable preserves the optical mode property during qubit propagation. This is a significant challenge, since many optical fiber systems exhibit photon attenuation and loss rates much larger than the coherence time of the associated qubits.
Experimental setups operating at wavelengths near 780 nm have been demonstrated using this principle, and modified photonic quantum logic gates remain the subject of ongoing investigation by many researchers and institutions.7-9 For example, recently developed 4 × 10 mm photonic qubit devices that implement an 8-qubit quantum computer have become accessible through cloud-based interfaces.10 This includes efforts supported by Cisco’s new quantum research team to demonstrate optical qubits integrated into photonic circuits using aluminum gallium arsenide (AlGaAs) laser sources.11
It’s too early to say which of these approaches will emerge as the equivalent of solid-state semiconductor processing for conventional computer chips, but we can expect high-quality laser sources to play a pivotal role in any quantum computing architectures to emerge in the future.
REFERENCES
1. See https://mck.co/3i3qoaV.
2. See https://bit.ly/3MGa65Q.
3. M. Guzdial, Commun. ACM, 65, 2, 20–22 (Feb. 2022).
4. See https://bit.ly/35vnHfD.
5. C. D. Bruzewicz, R. McConnell, J. Stuart, J. M. Sage, and J. Chiaverini, NPJ Quantum Inf., 5, 102 (2019); https://go.nature.com/3w2hTFh.
6. D. Niemietz, P. Farrera, S. Langenfeld, and G. Rempe, Nature, 591, 570–574 (2021); https://go.nature.com/3q6O2aX.
7. B. Bartlett, A. Dutt, and S. Fan, Optica, 8, 12, 1515–1523 (2021); https://bit.ly/37bXPpp.
8. See https://bit.ly/37ffAUZ.
9. See https://bit.ly/3HUXILn.
10. C. Q. Choi, IEEE Spectrum (Mar. 5, 2021); https://bit.ly/35DOplZ.
11. See https://bit.ly/3pJNrvy.
About the Author

Casimer DeCusatis, Ph.D
IBM Distinguished Engineer & CTO
Dr. Casimer DeCusatis is an IBM Distinguished Engineer and technical executive based in Poughkeepsie, N.Y. He currently serves as Chief Technology Officer for IBM Systems Networking Strategic Alliances, and has played a leading role in developing data center network and I/O solutions, including extended distance connectivity. He is an IBM Master Inventor with over 100 patents, and recipient of several industry awards, including the IEEE Kiyo Tomiyasu Award, the Sigma Xi Walston Chubb Award for Innovation, the EDN Innovator of the Year Award, the Mensa Research Foundation Copper Black Award for Creative Achievement, the Penn State Outstanding Scholar Alumnus Award, and the IEEE/HKN Outstanding Young Electrical Engineer award (including a citation from the President of the United States and an American flag flown in his honor over the U.S. Capitol). He is co-author of more than 120 technical papers, book chapters, and encyclopedia articles, and editor of the Handbook of Fiber Optic Data Communication (now in its 4rd edition). He is a member of the IBM Academy of Technology and co-leader of the Academy study “Innovation Ecosystems”. Dr. DeCusatis received the M.S. and Ph.D. degrees from Rensselaer Polytechnic Institute (Troy, N.Y.) in 1988 and 1990, respectively, and the B.S. degree magna cum laude in the Engineering Science Honors Program from the Pennsylvania State University (University Park, PA) in 1986. He is a Fellow of the IEEE, Optical Society of America, and SPIE (the international optical engineering society), a member of the Order of the Engineer, Tau Beta Pi, Eta Kappa Nu, Mensa, and various other professional organizations and honor societies (http://www.decusatis.net/casimer/ ); he was recognized as one of Sigma Xi’s Distinguished Members during their 125th anniversary celebration. He is also Founder and Director of Hudson Valley FIRST Lego League (http://www.facebook.com/HudsonValleyFLL) which offers over 1,000 students each year the opportunity to pursue their interest in science and technology. His discussions on data networking are available on Twitter (@Dr_Casimer) or his data networking blog (https://www-304.ibm.com/connections/blogs/DCN/ ).