Advantages of high-repetition-rate femtosecond lasers
In the world of femto- and attosecond laser science, some say the higher the laser pulse energy, the better. Nonetheless, many laser researchers are familiar with the maddening situation when the energy dial is in the red, the laser power supply is slowly starting to smoke, yet the signal is still so weak that the measurement will take years. So yes, when given the chance, going for the highest pulse energy is a choice, but is it the wisest choice given the state of lasers developed in recent years?
For some applications, the answer is always yes. When the goal is polarizing a vacuum, performing nuclear fusion, or generating secondary radiation with the pithy efficiencies of a few parts per trillion, the only way is to buy the biggest, baddest laser your grant money can afford.
However, in many research areas, such a brute force approach does more harm than good. Often, it’s better to spread that energy over multiple pulses and get the same (or higher) average power, but at a higher pulse repetition rate. This article reviews the cases where high-average-power, medium-pulse-energy lasers can dominate over large brute-force high-energy systems.
Reason one: High output stability
Let’s start by stating an all-too-little-advertised fact that the solid-state femtosecond lasers that emerged in the past decade or two are far superior to the first chirped-pulse amplification (CPA) systems developed at the end of the last millennium. With power ranging in the tens of watts and pulse energies around 1 mJ, they can operate at repetition rates from single shots to several megahertz. Due to direct semiconductor laser array pumping, together with ingenious optical design, typical Yb:KGW CPA laser systems deliver superior stability. A compact footprint reduces sensitivity to mechanical vibrations, and water-cooled housings make them robust with respect to ambient temperature drifts.
The pump energy is derived not from a single, but from several tens of semiconductor lasers, so the individual stability of each plays a relatively minor role. Most importantly, when the laser repetition rate increases so that the period between pulses becomes smaller than the natural lifetime of the lasing transition in the active medium (600 µs in the case of Yb:KGW, which corresponds to 1.6 kHz repetition rate), the laser medium itself starts acting as a low-pass filter, smoothing out any instabilities arising from the pump. Accordingly, high-repetition-rate laser systems are characterized by very high-power and energy stability (see Fig. 1).
Reason two: Most experiments require multiple pulses
Usually, collecting experimental data requires averaging. It does not matter, if these signal photons come in large but infrequent explosions or small droplets that batter the detector one after another. If, in the duration of the experiment (say, 1 second), the same number of photons are collected, the eventual result (all other factors being equal) will be the same.
Of course, it is rarely as simple as that. The signal may have an energy threshold and unless it’s surmounted, the measurement will suffer. But high-repetition-rate femtosecond laser energies are in the range of 1 mJ or more.1 This energy is enough to produce plasma in air when tightly focused (see Fig. 2), and it is what the typical energy of Ti:sapphire CPA systems used to be 20 years ago. So, a modern Yb:KGW CPA laser is effectively a battery of 10-50 Ti:sapphire lasers of yesteryear—and each laser in that battery is 10X more stable than the older systems.Reason three: Most experiments don’t use all the available pulse energy
The largest reason for choosing a high-repetition-rate laser is the fact that in many situations, the experimental conditions preclude one from using all the available pulse energy. This section reviews such cases in different fields of research employing femtosecond lasers.
Nonlinear optics
The invention of lasers has birthed the field of nonlinear optics, the exploration of intricate interactions of light and matter at at the conditions when the electric field of light starts to rival Coulomb attraction between the electrons and atomic nuclei. In these interactions, transformed light acquires new frequencies and weird and wonderful spatial properties.2, 3 Nonlinear optics effects occur in a strictly defined range of light intensities. In the condensed phase experiments, the pulse energies corresponding to these intensities are in the range of microjoules.
A good example is the generation of white light continuum (WLC)—broadband spatially and temporally coherent radiation generated by focusing femtosecond laser pulses into a transparent medium (see Fig. 3). In bulk condensed media, the threshold of WLC generation is typically 1–50 µJ, depending on the wavelength of light and the properties of the medium.When exceeding this threshold by roughly a factor of 3, the neat effects are no longer observed: either the laser beam breaks down into multiple filaments, or breakdown (optical damage) of the medium occurs. This means that nearly all the laser pulse energy above the threshold is unusable. Thus, in order to produce as many WLC photons per unit time as possible, it is desirable to use lower energy pulses arriving at the medium.
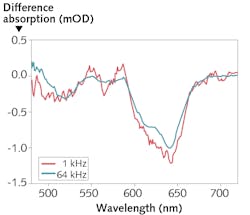
Furthermore, this energy dependence of WLC has an important corollary to femtosecond transient absorption spectroscopy. In fields such as biophysics, physical chemistry, photovoltaics, and semiconductor physics, researchers often choose WLC as the source of probe light in femtosecond pump-probe experiments. Such experiments use two laser pulses, one that excites the sample under investigation, and the other, arriving with controlled delay after the first, that measures the change in sample transmittance due to the excitation.
Attractive as a probe source, WLC covers a multi-octave spectral range, allowing the probing of different transitions in the investigated material. It is also very stable and easy to generate. Because the pump-probe experiment measures the ratio of probe intensities after the sample (excited to non-excited transmittance), the more photons in the probe pulse, the higher the sensitivity (it is impossible to detect a 1/1000 transmittance change with less than 1000 photons). Because the number of WLC photons registered per second is a linear function of repetition rate, the noise level of the experiment is significantly improved at high repetition rates (see Fig. 4).Generation of secondary radiation
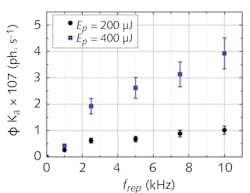
Generating secondary radiation imposes similar constraints on the energy of each incident pump pulse. Recently, Baguckis et al. have applied a multikilohertz Yb:KGW system for x-rays generation in a copper target.4 Results show that when the laser pulse energy is in the 200 µJ range, the brightness of generated x-rays scale linearly with the laser repetition rate (see Fig. 5).A shoebox-sized 20 W laser generates x-rays with brightness comparable to those generated by state-of-the-art Ti:sapphire CPA systems, delivering multi-millijoule pulses. Looking into the future, scaling a 200 µJ femtosecond laser to higher repetition rates is a significantly less-challenging task than scaling a 10 mJ laser to higher pulse energies. Accordingly, the future of tabletop x-rays may be at higher repetition rates.
Time-resolved spectroscopy
Femtosecond time-resolved spectroscopy is used in analysis of photosynthetic pigment-protein complexes,5 photoreceptor proteins,6 solar cells and their components,7, 8 light-emitting devices,9 and other light-sensitive molecular compounds.10 The natural condition for most of these systems is continuous illumination, where photons arrive one-by-one, not the bombardment by high-energy femtosecond pulses, where they arrive in large buckets. Ideally, one would illuminate systems with the type of light they need to function. However, if femtosecond time resolution is required (as it usually is), researchers may be forced to use the next best thing: low energy pulses. Here again, high repetition rate helps to accumulate enough signal to make meaningful scientific conclusions.
Perhaps the oldest known example, where intensity-dependent effects were misleading, comes from the study of photosynthetic light-harvesting complexes. In the late 1970s and early 1980s, several research groups studying excited state dynamics in chromatophores of purple bacteria were using the lasers of the time. Puzzlingly, all were reporting different excited-state lifetimes. It turned out that what they were looking at was nonlinear annihilation of excitations.11
It is the process when two excitations meet at a single chlorophyll pigment (see Fig. 6a), producing a higher excited state. Since this state decays almost instantaneously (~100 fs), the net result of such an encounter is the decrease in the number of excitations by one. In a large light-harvesting antenna, the more excitations you excite, the higher the chance they would meet and, hence, the faster the decay of the initial signal (see Fig. 6b).12 Fascinating as this effect is, it only manifests itself at very high excitation light intensities that never occur naturally. Therefore, to make meaningful conclusions about the naturally occurring light-harvesting, the experiments need to be done at minuscule excitation pulse energies. Higher repetition rates and correspondingly weaker pulses make this possible.Detection of single particles
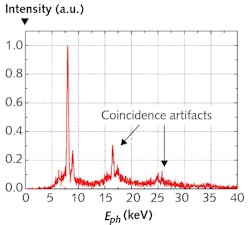
Sometimes it is not the laser, the sample, or the target, but the detection scheme that limits the excitation energy. In many detection schemes, single particles (photons, electrons, ions) are detected. For example, the cheapest and most widespread x-ray spectrometers employ the detection of charge generated in semiconductor die by a single x-ray photon. If two photons originating from the same laser pulse hit the detector at the same time, the spectrometer will erroneously determine two times higher photon energy (see Fig. 7). Similarly, if the products of light-matter interaction are photoelectrons (as in x-ray photoelectron spectroscopy), it is desirable to have just one electron per laser pulse. If multiple electrons enter the analyzer, their Coulomb repulsion distorts the measured energy values.In such single-particle detection experiments, the higher the laser repetition rate, the faster your signal counts are accumulating. A typical spectrum or decay curve needs around 10000 counts to combat discreet noise. When counting at 1 kHz repetition rate, it takes 10 seconds to measure, whereas at 100 kHz you are measuring 10 curves per second. Ten seconds does not sound like a lot, but when you change the duration of averaging to 10 hours, the alternative of getting the same result in 6 minutes suddenly becomes very attractive.
Summary
In summary, modern-day solid-state femtosecond lasers operating at multikilohertz repetition rates offer a unique combination of pulse energies high enough to produce almost all nonlinear-optical phenomena and, at the same time, they do it 10–100X faster than traditional CPA systems operated at 1 kHz or below. This results in unprecedented brightness of secondary radiation and helps to bypass the inherent fluence limitations imposed by the samples or detection systems. Together with the fact that these lasers are also more stable than their higher-energy counterparts, this makes them the tool of choice for modern research in spectroscopy, microscopy, nonlinear optics, and laser physics.
REFERENCES
1. See lightcon.com/product/pharos.html.
2. A. Dubietis et al., Phys. Rev. Lett., 92, 25 (2004).
3. D. Faccio et al., Phys. Rev. Lett., 96, 19 (2006).
4. A. Baguckis et al., Appl. Phys. B: Lasers Opt., 123, 12 (2017).
5. R. Berera, R. van Grondelle, and J. T. M. Kennis, Photosyn. Res., 101, 2–3, 105–118 (2009).
6. J. T. M. Kennis and M. L. Groot, Curr. Opin. Struct. Biol., 17, 5, 623–630 (2007).
7. T. M. Clarke and J. R. Durrant, Chem. Rev., 110, 11, 6736–6767 (2010).
8. O. E. Semonin et al., Science, 334, 6062, 1530–1533 (2011).
9. F. Liu et al., ACS Nano, 11, 10, 10373–10383 (2017).
10. N. P. Ernsting and T. Arthenengeland, J. Phys. Chem., 95, 14, 5502–5509 (1991).
11. L. Valkunas, V. Liuolia, and A. Freiberg, Photosyn. Res., 27, 2, 83–95 (1991).
12. V. Gulbinas et al., J. Phys. Chem., 100, 45, 17950–17956 (1996).
About the Author
Mikas Vengris
Professor/Chief Researcher, Vilnius University
Mikas Vengris is a Professor/Chief Researcher at Vilnius University (Vilnius, Lithuania).
Lukas Kontenis
Lukas Kontenis is an R&D Engineer at Light Conversion (Vilnius, Lithuania).
Jonas Berzinš
Jonas Berzinš is market development manager at Light Conversion (Vilnius, Lithuania).