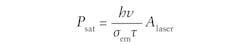Laser Design: Understanding and optimizing laser resonator designs: An overview

Many aspects of a laser’s performance depend substantially on the design of its laser resonator: the power-conversion efficiency, the beam quality, and the alignment sensitivity, for example. Therefore, it is essential—although often not easy—to develop optimized laser resonator designs.

This article is intended to give an overview on the crucial aspects of laser resonator design. Bulk laser resonators are considered here, where the resonator modes are determined by a balance of focusing effects (for example, from curved laser mirrors) and the diffraction of light in free-space regions. Figure 1 shows two examples: a linear and a ring resonator. Fiber lasers and other waveguide lasers, in which the mode properties are determined by waveguide effects, are outside the scope of this article.

The role of resonator modes

The most-essential properties of a laser resonator can be understood as properties of its resonator modes, which need to have appropriate mode radii in the laser gain medium (in this example, a laser crystal). It is often not sufficient to fulfill such a condition only for some nominal configuration: for robustness, the mode radii should not react too sensitively to changes of resonator arm lengths or changes of the thermal lens in the laser crystal.

The resonator-design process is usually done in two distinct steps. First, suitable resonator mode parameters are determined; in particular, the required mode radii at certain locations—for example, in the laser crystal and at the laser output, and possibly in other optical components where they are relevant—are determined. Second, a resonator design is sought in which the modes have those properties. This means that a decision must be made on a certain resonator architecture, as well as suitable parameters (arm lengths, curvature radii, and so on) for it.

The first step also involves some laser physics: the laser beam diameter in the gain medium must be chosen to produce an appropriate level of gain saturation, which is related to a certain ratio of pump power to pump threshold power of the laser. Obviously, it would be inefficient to design a laser for some beam size in the gain medium and find out only after building the prototype that there is not enough laser gain for operation reasonably above the threshold. The goal should be to find a design that needs only minimal refinements later on—that is, one that minimizes the amount of work in the laboratory related to procuring of parts that, in the end, wouldn’t be used anyway.

Example: Appropriate beam radius for a CW laser

As a simple example, an end-pumped continuous-wave (CW) solid-state laser, such as with Nd:YAG and a linear resonator, is considered. From the intended output power level and a reasonable choice of output-coupler transmission (for example, 10%), the intracavity laser power can be calculated. The beam radius in the laser crystal should then be chosen such that the double-pass saturation power (which is half the single-pass saturation power) is around one quarter of the circulating laser power—this will lead to operation at (1 + 4) = 5 times above the laser threshold. (For quasi-three-level gain media like Yb:YAG, this calculation would be somewhat more complicated.) Note that the single-pass saturation power can be calculated as:

where hv is the laser photon energy, σ_em is the emission cross-section at the laser wavelength (for Nd:YAG at 1064 nm, this is 28 × 10^-24 m²), τ is the upper-state lifetime (for Nd:YAG, this is 230 µs), and A_laser = πr²_laser is the beam area in the laser crystal.

For a laser output power of 10 W at 1064 nm, the beam radius in the laser crystal is about 0.7 mm. Of course, this value can be changed somewhat—for example, when using a different output coupler transmission or operating further above threshold. For a Ti:sapphire laser, where the saturation intensity is much higher, the calculated beam radius would be substantially lower.

Deciding on the mode radius

So far, what has been calculated is the required beam radius in the laser crystal, which is not necessarily identical to the mode radius. If the laser is designed for diffraction-limited beam quality, these values should be similar, and the fundamental resonator mode would cover the whole pumped area. Higher-order transverse modes will then have a reduced overlap with the pumped area, and thus a lower gain, so that they cannot participate in the laser process. (The fundamental modes will saturate their gain such that it can just compensate the resonator losses; the gain for higher-order modes is then too low for lasing.) A slightly larger mode area may result in somewhat safer suppression of higher-order modes, but it would increase the threshold power and might cause increased problems with thermal lensing. Particularly for high-power lasers, the design cannot go far in that direction.

For high-power lasers operated with large beam areas, serious problems can be encountered when designing for optimum beam quality. The mode radius will then substantially depend on the dioptric power of the thermal lens of the laser crystal so that the laser may work only in a narrow range of pump powers, which often cannot be accurately predicted. Aberrations of the thermal lens can also have substantial effects in that regime.

The alignment sensitivity of a resonator with large modes is typically quite high. Even slight tilting of a laser mirror, for example, can move the modes out of the pumped area, which affects the power-conversion efficiency as well as the beam quality.

Although such problems can be mitigated to a substantial extent with a good resonator design, more and more problems will arise as the power level is increased. Therefore, the resonator can be intentionally designed for smaller mode radii, which has several consequences. First, some combination of transverse modes will lase, which in total will cover the full pumped area. The beam quality will be reduced accordingly, which is acceptable for some applications. Second, the power-conversion efficiency will typically be somewhat increased. Third, the stability zones of the resonator (see below) will become wider—as a result, the laser can be operated over a substantial range of powers, even if thermal lensing is strong. Further, the alignment sensitivity can be substantially reduced, which contributes to a robust laser design.

Stability zones

Outside the stability regions, the result is an “unstable resonator” with modes that have far more complicated properties. A laser is rarely operated in that regime because of the large diffraction losses.

Additional constraints

Concerning the determination of mode radii in the gain medium, various additional constraints may occur—for example, for an actively Q-switched laser, where appropriate mode radii are also required at the Q switch: small enough to avoid beam clipping, but also large enough to avoid excessive optical intensities. Similarly, the mode radius at a saturable absorber in a passively mode-locked laser needs to be chosen appropriately. Constraints can also exist on the resonator length, influencing the pulse duration in case of Q switching or the pulse repetition rate in case of mode-locking.

Finding a resonator design

Once the required mode properties have been determined, the remaining task is to find a resonator design that meets those criteria—this is often the most difficult step. First, a decision must be made on the type of resonator architecture—for example, can it be a simple two-mirror resonator, or are one or more curved folding mirrors required? Should the laser crystal be placed close to an end mirror, or between two focusing mirrors? Where should additional elements for wavelength tuning, Q switching, or other purposes be inserted? Where should the output be extracted? These decisions will typically require some experience and might have to be revised later on if it is found that the requirements cannot be met.

Here, numerical resonator design software is generally used. It is normally sufficient to use software based on the paraxial optical approximation, working with the ABCD matrix algorithm (or actually an extended form with ABCDEF matrices for calculating the alignment sensitivity). Still, the dependence of mode properties on the resonator parameters (curvature radius of mirrors, distances between elements, and so on) is generally too complicated for working without numerical software. A typical approach is to define a figure of merit, which would be zero in the ideal case (with all requirements perfectly met) and contains positive “penalties” for all nonideal properties—for example, concerning mode radii for some range of dioptric powers of the thermal lens, total resonator length, and such. The software can then automatically adjust various free resonator parameters such as to minimize the figure of merit. Because a multidimensional parameter space with many local optima is often encountered, a Monte-Carlo algorithm may need to be used, starting numerical optimizations at many randomly chosen parameter sets.

If the used software is sufficiently flexible, advanced optimization strategies are possible. For example, a figure of merit may be constructed in the following way:

1. For any set of mirror curvatures and arm lengths, the dioptric power is calculated such that the resonator is operated where the mode radius in the gain medium acquires its minimum value—and this in the one stability zone having the lower alignment sensitivity.

2. The deviation of the calculated dioptric power to the expected dioptric power is used for an additional penalty in the figure of merit.

With such a strategy, a design is automatically obtained that operates in the wanted stability zone, having a zero derivative of the laser mode radius with respect to the thermal lens dioptric power.

Note that resonator properties are also subject to fundamental physical limitations. For example, a short resonator with a large mode area over a wide range of dioptric powers of the thermal lens is not possible. The width of a stability region depends on its minimum mode size, and diffraction needs to be strong enough (that is, it must act over a sufficiently long propagation length) to enforce a sufficiently large minimum mode size. Therefore, large mode area resonators for high-power lasers generally need to be longer. The understanding of such limitations helps appropriate resonator architectures to be found more quickly.

Build up competence, possibly with external support

Laser resonator design requires advanced expertise concerning resonator properties, laser physics, and design strategies. A laser designer should obviously try to acquire such expertise, possibly making use of external support. For example, advanced resonator design software should come with competent technical support explaining not only the handling of the software, but also giving advice on how to determine required resonator mode parameters and how to find suitable designs based on them.