NONLINEAR OPTICS: Photonic-crystal fibers are selectively filled with nonlinear liquids
MARIUS VIEWEG, TIMO GISSIBL, and HARALD GIESSEN
The concept of filling the holes in a photonic-crystal fiber (PCF) to modify the fiber’s properties has gained a tremendous amount of interest in different optical fields. It is possible to use gases, metals, and liquids as filler materials.1–4 In nonlinear optics, liquids are most interesting because of their potential to generate high optical nonlinearities due to their large nonlinear coefficients. It is highly desirable to combine the structure of a PCF with the nonlinear optical properties of a liquid to gain complete control over dispersion and high nonlinearity simultaneously.5
We have developed a method to selectively fill PCFs with nonlinear liquids such as toluene or carbon tetrachloride (CCl4), and have measured solitonic spectral broadening in these fibers.6 The creation of a liquid waveguide array in a PCF shows the versatility of our technique.
Holes filled by capillary forces
A 3D direct laser-writing technique is used to selectively seal single holes.7 First, all holes are covered with an epoxy polymer (see Fig. 1). In the second step, the polymer is crosslinked by two-photon absorption of a focused femtosecond-laser pulse. The two-photon process allows 3D control over the cured volume such that the size of the voxel scales with the intensity. The challenge of this process is the correct addressing of the holes to avoid affecting the neighboring holes. To conveniently fabricate such fibers, we have automated the direct laser-writing process.
In the next step of the fabrication process, various liquids can be used to fill the fiber holes, with the choice of liquid limited only by toxicity and transparency. By using carbon disulfide, it is possible to enhance the nonlinearity by a factor of about 200 compared to fused silica. We chose toluene and CCl4 for our experiments because they present a good compromise between nonlinearity and nontoxicity. Also, the refractive indices of toluene and CCl4 are 1.48 and 1.45, respectively, which is slightly higher than the refractive index of the fiber material. Therefore we can use toluene and CCl4 in fibers with a small d/Λ ratio, where the effective refractive index of the holey region becomes similar to fused silica, without losing guiding properties. In particular, CCl4 allows for propagation of the fundamental mode in almost all cases.
The holes are filled by capillary forces. By choosing the appropriate hole diameter, hole-to-hole distance, and liquid, one can adjust the zero-dispersion wavelength for the experiment over a huge wavelength range that spans from the near IR to 600 nm. The 2D structure of a PCF can be utilized to arrange several waveguides in an arbitrary pattern to obtain discrete optical-waveguide arrays with desired properties.Two different filling patterns
The simplest filling pattern is a single-strand structure. In this case, just one hole of the PCF is left open and this single strand is filled with the liquid. Light from a 250 fs laser source at 1030 nm was coupled into the device and propagation of the fundamental mode was observed.
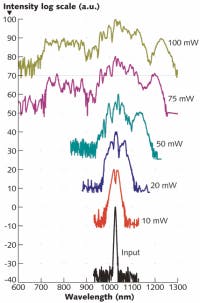
To tailor the liquid-filled PCF such that propagation takes place in the anomalous-dispersion regime (meaning in this case that the zero-dispersion wavelength is smaller than 1030 nm), we used the highly nonlinear liquid CCl4, which has a nonlinear refractive-index coefficient six times higher than that of fused silica. Output spectra were measured as a function of input intensity (see Fig. 3). For low pump powers, the spectral broadening is mainly caused by self phase modulation, while for higher pump powers, supercontinuum generation due to soliton formation, fission, and Raman processes takes place.
Applications of the selectively filled PCF include spatio-temporal nonlinear propagation with specific tailored properties such as nonlinear all-optical switching, as well as the generation of spatio-temporal solitons (“light bullets”).8,9 Highly interesting effects arise due to the time-delayed response of the liquid, which stems from delayed reorientation of the liquid molecules.10–12 Furthermore, purely nonlinear lattices can be created.13 Additionally, the method is suited for selective filling of several different liquids, or for creation of highly birefringent liquid-filled PCFs using (for example) liquid crystals. Another possibility is to selectively infiltrate different gases for higher-harmonic generation. Several approaches are applicable to the field of biosensing.14
REFERENCES
1. F. Benabid et al., Science, 298, 399 (2002).
2. M.A. Schmidt et al., Phys. Rev. B, 77, 033417 (2008).
3. B.T. Kuhlmey et al., J. Lightwave. Technol., 27, 1617 (2009).
4. P.D. Rasmussen et al., Opt. Exp., 16, 5878 (2008).
5. R. Zhang et al., Opt. Exp., 14, 6800 (2006).
6. M. Vieweg et al., Opt. Exp., 18, 25232 (2010).
7. S. Maruo et al., Opt. Lett., 22, 132 (1997).
8. F. Ye et al., Opt. Exp., 17, 11328 (2009).
9. S. Minardi et al., Phys. Rev. Lett., 105, 263901 (2010).
10. R. Raja et al., J. Opt. Soc. Am. B, 27, 1763 (2010).
11. S. Pricking and H. Giessen, Opt. Exp., 19, 2895 (2011).
12. C. Conti et al., Phys. Rev. Lett., 105, 263902 (2010).
13. Y. Kartashov et al., Opt. Lett., 34, 770 (2009).
14. T. Euser et al., Opt. Lett., 34, 3674 (2009).
Marius Vieweg,Timo Gissibl, and Harald Giessen are at the 4th Physics Institute, University of Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany; e-mail: [email protected].