Soliton transmission is a balancing act that offsets two major classes of pulse degradation in optical fibers to improve the quality of signal transmission. One type of degradation is the dispersion that causes pulses to spread in duration as they travel through long lengths of fiber. The other is the nonlinear effects that arise from power-dependent interactions of signals with each other and with the fiber. In most circumstances, the two effects combine to make matters worse, but if optical pulses have certain shapes and power levels, the two effects can cancel each other out—at least to a first-order approximation. Pulses that meet these conditions are called solitons.
One powerful allure of solitons is their inherent robustness for high-speed transmission over long distances. Solitons do suffer attenuation, but their shape can be made inherently stable over long lengths of fiber. This offers a way to keep dispersion and nonlinear effects from degrading signal quality, a significant problem at speeds of 10 Gbit/s that grows more severe at higher transmission speeds. These properties have led developers to work on soliton systems both for long-haul 10-Gbit/s systems, and for future 40-Gbit/s systems.
Origins of solitons
Solitons were first recognized in the form of solitary waves that traveled along nineteenth-century canals. Mathematical analysis revealed the phenomenon was a general one in certain circumstances. In 1973, Akira Hasegawa and Yuji Kodama showed theoretically that soliton pulses could propagate in optical fibers. Linn Mollenauer generated fiberoptic solitons experimentally in 1980, but initially the idea seemed mainly of academic interest because early fiberoptic systems used electro-optic repeaters, which limited the distance that optical pulses traveled before regeneration.
Optical amplification made solitons far more attractive. In 1985, Mollenauer demonstrated soliton transmission using Raman amplification, and in a 1988 experiment he extended the transmission distance to 4000 km using Raman amplification in a recirculating loop. The erbium-doped fiber amplifier opened new possibilities, allowing Mollenauer to transmit soliton pulses at 5 Gbit/s through a total of 6000 km of fiber at Bell Labs (Holmdel, NJ). Higher speeds and longer distances followed, but wavelength-division multiplexing leaped ahead and became the technology chosen to multiply fiber capacity in the mid-1990s.
Now solitons are returning to meet growing needs for longer-distance transmission at higher speeds. "We can easily provide error-free transmission over 100 or more channels at 10 Gbit/s each" for terrestrial distances beyond 5000 km with solitons and purely Raman amplification, said Mollenauer. Several companies are developing 10-Gbit/s soliton systems to avoid the need for regeneration in ultralong-haul systems. Solitons may prove even more vital at 40 Gbit/s, because they can deal with nonlinear effects that are inevitable at such high speeds, said Mark J. Ablowitz of the University of Colorado in Boulder.
Soliton basics
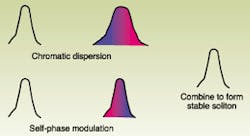
The mechanism by which solitons stabilize their own pulse shape is best understood by starting with a simple single-channel system in which signals experience both chromatic dispersion and self-phase modulation. The two effects are independent, so they can be considered separately.
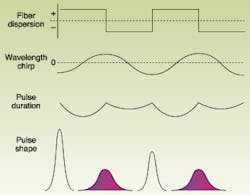
Chromatic dispersion arises from the range of wavelengths present in all optical signals. The group velocity of light signals through a fiber varies with the wavelength, largely—but not entirely—because refractive index also depends on wavelength. If an instantaneous pulse directs all wavelengths into the fiber simultaneously, the pulse will spread gradually because some wavelengths travel faster than others. Depending on the sign of the chromatic dispersion, the long wavelengths are ahead of the short ones or vice versa, spreading out the duration of the entire pulse (see Fig. 1). The amount of pulse spreading caused by chromatic dispersion increases linearly with the distance the signal travels through the fiber. If chromatic dispersion totals 1 ps after 1 km, it would total 2 ps after 2 km, and so on.
Self-phase modulation arises because the refractive index of glass includes a term that is the product of the nonlinear refractive index n2 and the instantaneous signal intensity I(t). This causes the refractive index to vary as the power rises and falls, causing phase and frequency shifts that vary during the pulse. Self-phase modulation does not stretch out the duration of the pulse, but it does induce a wavelength chirp, which shifts light to short wavelengths at one end of the pulse and long wavelengths at the other. The effect is modest but significant at the intensities present in fiberoptic systems, but can be quite large at extremely high intensities.
Put the two effects together in a suitable optical fiber and they can offset each other for pulses of suitable shape, power, and duration. In the simple case of a length of uniform fiber, the two effects occur simultaneously, maintaining pulse shape along the entire length. Although soliton pulses have characteristic shapes and power levels, it is not vital to start with the precise shape. As the pulses travel through the fiber, pulses of approximately the right characteristics assume soliton shape if their peak intensity is 0.25 to 2.25 times the ideal level. Optical amplification is needed eventually to compensate for fiber attenuation if the pulses are to remain at the power levels needed to sustain a soliton.
Dispersion-managed solitons
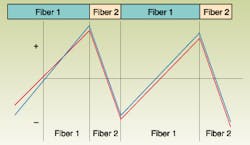
Early demonstrations produced what are now called "classical" solitons by transmitting pulses through a single uniform type of fiber, amplifying the optical pulse where necessary. It seemed an attractive way to achieve high data rates, but it couldn't keep up with advances in wavelength-division multiplexing, and further research revealed serious limitations. Collisions in which soliton pulses overlap can cause cross-phase modulation that can disrupt transmission. Single-channel systems can avoid collisions if pulses are separated by an interval of at least 4 to 5 times the pulse duration. However, the variation of fiber dispersion with wavelength makes collisions inevitable in WDM systems that use classical solitons, because some wavelengths will catch up with others. Other problems arose from Gordon-Haus jitter (which causes random variation in pulse spacing) and four-wave mixing.
Dispersion management overcomes these problems by splicing together alternating sections of two fiber types having different dispersion properties to produce dispersion-managed solitons (see Fig. 2). As in dispersion compensation for conventional fiberoptic systems, a major goal is to reduce total dispersion of the length of fiber by combining fibers so their individual dispersions largely cancel out. Typically these systems use two different types of fiber having opposite signs of dispersion. Lengths of the segments of the two types are picked so the cumulative dispersion through one pair of segments is close to zero. The length of the pair of fiber segments, called the dispersion map length, is a key design parameter. As with classical solitons, the pulses require periodic amplification for long-distance transmission.
Dispersion and nonlinear effects cancel each other over the whole length of dispersion-managed solitons as well as for classical solitons, but the effects are not identical. Classical solitons remain the same along the length of the system because the dispersion and nonlinearities offset each other continually. The shape of dispersion-managed solitons oscillates along the fiber with a period equal to the dispersion map length (see Fig. 3).
"Dispersion management does lots of very good things," said Mollenauer. It allows designers to adjust dispersion so it is quite uniform across a wide band of wavelengths—a capability that is vital for WDM, but virtually impossible using only a single type of fiber. Pulse energy can be higher than that of classical solitons, helping to prevent spontaneous emission noise from degrading long-haul systems. Overall, it gives designers extra degrees of flexibility that allows them to enhance system performance.
Pushing to higher speeds
Standard commercial 10-Gbit/s WDM systems are based on non-return-to-zero (NRZ) linear transmission. Dispersion-managed soliton systems are in the running to stretch transmission distances at 10 Gbit/s and to enable future 40-Gbit/s systems. They are inherently return-to-zero (RZ) systems, with relatively long intervals required between the brief pulses. However, Ablowitz said the central difference between solitons and conventional NRZ or RZ transmission is that solitons take advantage of system nonlinearities while conventional systems try to limit nonlinearities. That poses serious challenges at 40 Gbit/s, where higher speeds and power levels combine to make nonlinearities inevitable.
Wavelength-division-multiplexed soliton transmission at 10 Gbit/s is "a mature technology," said Mollenauer. "We can easily provide error-free transmission over 100 or more channels at 10 Gbit/s each, and ultimately as much as 1.6 Tbit/s, on 160 channels, in purely all-optical mode over more than 5000 km." That's based on amplification every 80 to 100 km, standard in North American terrestrial transmission. His group has demonstrated soliton transmission over those distances using all-Raman amplification, which reduces noise 5 to 6 dB below the levels from erbium-doped fiber amplifiers, and gives flat gain over wider bands. Dispersion-compensating fibers serve as his Raman gain medium; their small cores increase power density, so they can be pumped with 300 to 400 mW from diode lasers.
Tougher challenges face developers working on 40-Gbit/s transmission. "Both solitons and quasi-linear formats are very promising," said Ablowitz. Power requirements are 6 dB higher than at 10 Gbit/s because the bit intervals are only 1/4 as long, so "you have to deal with nonlinearity in one form or another." Although laboratory demonstrations have achieved some impressive results, Ablowitz and others are developing mathematical models for engineers to use in predicting performance and designing systems.
It's too early to predict a winner, and some observers question the push to 40 Gbit/s at a time when Wall Street is complaining of a "fiber glut." Nobody expects the technology to be easy. Yet, said Mollenauer, "When the day comes that we can install dispersion-managed cable, 40-Gbit/s dispersion-managed solitons will work very well."
ACKNOWLEDGMENTS
Thanks to Mark Ablowitz and Linn Mollenauer.
REFERENCES
- A. Hasegawa and Y. Kodama, Solitons in Optical Communications (Oxford University Press, 1995).
- P. V. Mamyshev, "Solitons in Optical Fiber Communication Systems," in Michael Bass ed., Optical Society of America: Handbook of Optics, Vol. IV: Fiber Optics & Nonlinear Optics (McGraw-Hill, 2001).
