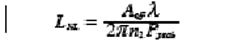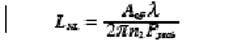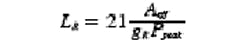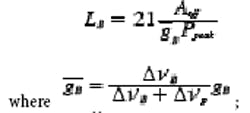Pumping schemes use large-mode-area components
Both co- and counter-pumped amplifiers can readily be assembled with large-mode-area fibers; a beam quality M2 of 1 can be achieved without a significant loss in efficiency. This capability allows considerable freedom in the design of high-power, robust fiber lasers and amplifiers.
Laser sources delivering high-peak-power pulses at 1060 and 1550 nm are useful for applications that include laser rangefinding, obstacle avoidance, microburst detection for aircraft, wind or turbulence sensing, target designation, and machining, as well as frequency conversion into the mid-IR for countermeasures. These applications are currently addressed by solid-state lasers; however, fiber lasers are making inroads in this market, largely because of the accessibility of 1060- and 1550-nm operation with erbium (Er) or erbium-ytterbium (Er-Yb)-doped fibers.
Some applications require high peak power and narrow linewidth simultaneously, which would seem to preclude optical fibers because of their inherent nonlinear effects in silica that cause the optical pulse to spread, scatter, and reflect, and thus degrading the beam before it leaves the laser. Large-mode-area (LMA) fibers have been developed with large-diameter cores that increase the power thresholds of nonlinear effects. Though LMA fibers suffer from other problems-such as bend sensitivity and few-mode guiding-we have studied co- and counter-pumping configurations and developed techniques to overcome these issues, demonstrating various pump geometries to show how both high-peak- and average-power fiber sources can now be manufactured.
Limiting nonlinear effects
Three main nonlinear phenomena occur when high-power pulses propagate within the core of an optical fiber: nonlinear phase shifts, Raman scattering, and Brillouin scattering.1, 2 They can all be characterized by a nonlinear length parameter, which defines the maximum propagation length of a pulse before it is seriously affected by the nonlinear effect.
Self-phase modulation and four-wave mixing widen the spectrum of the signal. Depending on the application, this broadening may or may not be detrimental to the overall system. Detrimental effects can also show up as losses due to spectral filtering in the overall system, on either the emitter or the receiver side. The nonlinear length is given by:
null
where Ppeak is the peak pulse power, Aeff the effective area of the mode (approximately the area of the fiber core), λ the pulse wavelength, and n2 the nonlinear coefficient of silica.
Stimulated Raman scattering (SRS) shifts some of the energy toward a longer wavelength known as the Stokes wave. An anti-Stokes (shorter-wavelength) wave can also occur, but the process is much less efficient. If spectral filtering is used in the amplifier to suppress amplified spontaneous emission for example, SRS acts as a loss source. This is equivalent to a limiter for the signal intensity. The nonlinear Raman length is given by:
where the Raman gain gR = 1 × 10-13 m/W.
Stimulated Brillouin scattering is caused by acoustic-vibration modes created in the glass by intense signals. The Brillouin gain depends on the signal linewidth; hence, the signal linewidth must be made wide enough either by using short pulses or by broadening through amplitude or phase modulation. Typically, a linewidth or equivalent linewidth of a few hundreds of megahertz is sufficient to minimize the Brillouin backscattering. The Brillouin shift is on the order of 10 GHz and a signal reflectivity close to 100% is possible. For narrow-linewidth laser sources, SBS is the nonlinear process with the shortest nonlinear length and thus is the main concern in our 1550-nm fiber laser.
The stimulated Brillouin scattering nonlinear length is given by:
where gB = 5 × 10-11 m/W, ∆νB is the Brillouin bandwidth (∆νB = 30 to 50 MHz for fiber), and ∆νP is the signal linewidth.
The nonlinear lengths are all inversely proportional to power density (peak power over effective area of the waveguide mode). To attain high-peak-power pulses, one must increase the effective area (the core size of the fiber) while making sure the total length of the laser is shorter then any nonlinear length. The use of LMA fiber reduces these nonlinear effects; however, even with low-numerical-aperture (NA) fibers, when the core becomes large, the fiber is no longer single-mode and few-mode propagation becomes an issue for the output quality of the laser, resulting in a degraded M2 (beam-quality) parameter. The solution must thus be a compromise between pulse power and core size with the fiber length as short as possible.
Co- and counter-pumping experiments
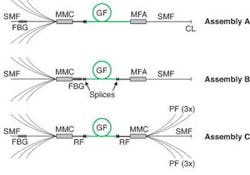
Three different configurations of fiber lasers-assemblies A, B, and C-were investigated (see Fig. 1). In all cases, a multimode pump-and-signal combiner was used to couple the pump light into a double-clad fiber (DCF). In the so-called (6 + 1) × 1 configuration, six pump fibers and one signal fiber are coupled to the inner cladding and the core of the DCF, respectively.3
The pump fibers are standard 200/220-µm fiber with an NA of 0.22. The signal input fiber is a single-mode fiber (for example, Corning HI-1060) and the double-clad relay fiber has a core diameter of 20 µm (NA of 0.06) and an inner cladding diameter of 400 µm (NA of 0.46). The relay fiber is spliced to a Yb-doped gain fiber (Nufern LMA-YDF-20/400) of similar geometry and a length greater than 8 m.
Because the 20-µm core supports more than one mode, the gain fiber is coiled with a radius of 5 cm to suppress the lasing action of higher-order modes.4 On the output side, the single-mode operation is enforced through the use of single-mode fiber. Assemblies A and B use mode-field adapters (MFAs) to provide a low-loss transition of the fundamental mode from the DCF signal core to the single-mode fiber. For each assembly, the laser cavity is formed between a fiber Bragg grating as the high reflector and a straight cleave of the single-mode fiber as the output coupler. In assemblies A and C, a chirped grating with a reflectivity of greater than 99% and a bandwidth of 5 nm was written into a Corning HI-1060 fiber. Assembly B used a grating in the relay fiber core with a reflectivity of 89% and a 0.14-nm bandwidth.
The fiber assemblies were tested using three fiber-coupled pump-diode modules at a wavelength of 976 nm with each module delivering a total power of about 45 W in two fibers, yielding a total pump power of 138 W in six fibers. The diode modules were simply spliced to the fiber-laser assemblies without the use of isolators.
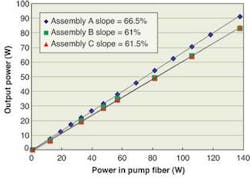
All fiber-laser assemblies exhibited a low threshold-pump power of around 1 W. The achieved output powers were 91, 83, and 84 W for assemblies A, B, and C, respectively (see Fig. 2). All curves show very linear behavior without roll-off. Assembly A had the highest slope efficiency of 66.5%, which is based on the pump power in the pump fibers. Therefore the slope efficiencies include the (relatively low) coupling loss from the pump fibers to the gain fiber. The output spectra, which were measured using an optical spectrum analyzer, showed good agreement with the measured reflection spectra of the fiber Bragg gratings. Assembly A was emitted at a wavelength of 1075 nm and the others at 1080 nm.
At high power, there was only slight evidence of self-phase modulation. At 83 W of output power, the full width at half maximum of the emission spectrum widens by about 50% as compared to low powers. There was no stimulated Raman scattering present for any of the configurations. The intensity noise of assembly C was characterized using a 1‑GHz photodetector and a 500-MHz oscilloscope, indicating very stable operation with a standard deviation of 1%.
Assembly C also offers further scaling in output power, because only half of the pump ports are used. Potential issues with the high power density at the output cleave (HI-1060 mode-field diameter of 6.2 µm) can be overcome through the use of end caps. Alternatively, LMA fibers can be used, which further suppress nonlinear effects.
These three different single-stage, single-mode fiber-laser configurations show outputs of up to 91 W. The slope efficiencies are up to 66.5% with threshold pump powers around 1 W. There was no evidence of stimulated Raman or Brillouin scattering and only a small amount of self-phase modulation. These designs allow scaling to higher output power.
Fiber amplifiers
The choice between co- and counter-pumping for an amplifier system is not always an easy one. Traditionally, the counter-pump configuration is chosen to allow the most pump power at the end where it is needed, and to reduce the nonlinear losses in a high-power pulsed system due to the fact that the pulse energy reaches its nonlinear regime toward the end of the fiber. Conversely, in the co-pumping case, the pulse intensity grows more rapidly at the beginning of the fiber and reaches its nonlinear regime earlier on in the fiber.
Counter-pumping topologies can result in a loss in overall system performance, due to the greater complexity at the laser output. The co-pumped output is the simplest, having potentially the shortest useable output fiber (important for high-peak-power systems where access is required to the output fiber face), and potentially the best M2, as there is nothing to degrade the beam after it exits the fiber.
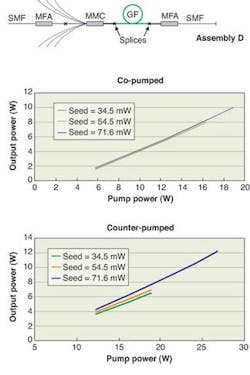
A configuration (assembly D) was assembled to investigate the continuous-wave behavior of co- and counter-pumped amplifiers in a fair test, as in both cases only pure single-mode output power is measured (see Fig. 3). Since both ends of the amplifier are single-mode fibers, the positions of the source and detector were simply reversed to change from co-to counter-pumping configuration. For each mode of operation, the pump and seed powers were adjusted, and both forward and reverse power and spectra were monitored.
The losses are not symmetric in the assembly, the loss in the MFA and multimode combiner (plus splices) was about 1.3 dB, which leads to a slightly lower counter-pump efficiency, whereas the loss in the output MFA alone (and splices) was about 0.8 dB and is responsible for the somewhat higher efficiency in the co-pump configuration.❑
REFERENCES
1. G. P. Agrawal, Nonlinear Fiber Optics, 2nd edition, Academic Press (1995).
2. R. H. Stolen, Proc. IEEE 68, 1232 (1980).
3. F. Gonthier et al., “High Power All-Fiber components: The missing link for high power fiber lasers,” Photonics West 2004.
4. J. P. Koplow et al., Opt. Lett. 25, 442 (2000).
5. M. Jäger et al., paper JWB59, CLEO 2005, Baltimore, MD (2005).
François Gonthier, Alain Villeneuve, Matthias Jäger, and Nigel Holehouse