Nonlinear dynamics pose challenge and opportunity

Guillermo Carpintero and Horacio Lamela

Our current understanding of nonlinear dynamics allows us to avoid nonlinear behaviors and, more recently, to even find applications for them.

The first laser action in semiconductors was reported by several research groups in 1962 and was followed 10 years later by the first commercially available laser diode, which started the quest to meet the needs of a seemingly endless list of applications (see Laser Focus World, April 2000, p. 81). Theoretical as well as experimental studies on the modulation characteristics of these devices was started as early as 1964 and was the forerunner to the work that has led up to our current understanding of these characteristics, which is presented here.^1,2

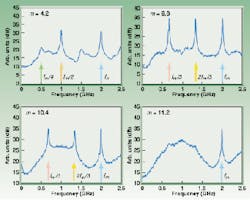
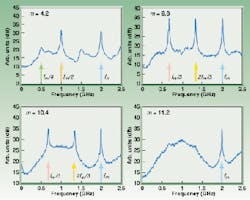
FIGURE 1. Averaged FFT spectra of the modulated laser (at frequency f_m) show different amplitudes of modulation (m).

On the theoretical side, a key factor in the study of laser diode dynamics has been the introduction of suitable models to explain the behavior of the device. Today, the most common description of a laser is based on the rate-equation approach proposed by Statz-De Mars, in which a set of ordinary differential equations accounts for the time evolution of the laser variables: the carrier and photon densities within the active layer (where lasing action takes place in the device).³ This model provides a useful description of the device since it accurately predicts the frequency of the laser's relaxation oscillations at any given bias level, a key factor in optical communication applications.⁴ The frequency constitutes an important laser parameter since it establishes the upper limit for the modulation bandwidth of the device.

A striking report by H. Haken in 1975 pointed out that the rate-equation model used to describe a laser is equivalent (in mathematical jargon, isomorphic) to the Lorenz model. This report had important implications since the Lorenz model, a simplified description of atmospheric dynamics, is today's paradigm in nonlinear dynamics. In fact, the first report of chaotic behavior in lasers appeared in 1982 on a Q-switched CO2 laser.⁵

The second threshold
A turning point in the analysis of lasers was reached when bifurcation theory became a fundamental tool in the study of their dynamics. Early studies of the nonlinear regimes resulted in the definition of the laser's second threshold. The first threshold is the pumping level required for lasing action to start, and the second is the point at which nonlinear behaviors appear. Beyond this level of pumping, the laser was thought to become useless. Today, our understanding of the nonlinear dynamics allows us to avoid nonlinear behaviors and, more recently, even to find applications for them.

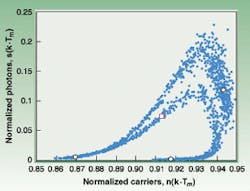
FIGURE 2. State space diagram shows the samples taken to the dynamics of the modulated laser diode (blue dots), and of two different periodic regimes involved: 3T_m-periodic behavior (period tripling, in dark circles) and an unstable T_m-periodic behavior (red square).

Extensive studies on the nonlinear dynamics of laser diodes have concentrated mainly on two different configurations—directly modulated and external feedback. While direct-current modulation of laser diodes is an important technique in fiberoptic communication systems because it allows for easy translation from an electrical to an optical signal, the external-feedback configuration is also significant because it enables the laser linewidth to be reduced. In this case, part of the light emitted by the laser is reinjected into the device. However, it has been demonstrated theoretically and experimentally that, under certain circumstances, both configurations may exhibit irregular types of behavior eventually leading to deterministic chaos. (The term "chaos" was coined for very complex regimes where the evolution of the system seemed erratic, without any definite period. Its deterministic character indicates there is no contribution from random sources to the erratic dynamics).

To determine the circumstances under which nonlinear behavior occurs, and to distinguish between chaotic regimes and noise, we rely on bifurcation theory, which has enabled an unprecedented understanding of these devices. First, however, we must learn the language and methods of this discipline—which is not new, as it was started by H. Poincarè, a French mathematician, at the end of the last century. In what follows, we address the dynamics of modulated laser diodes.

Experiments vs. theory
Early studies on the dynamics of directly modulated laser diodes, based on the rate-equation description of the device, predicted that deterministic chaos would appear after a sequence of period-doubling bifurcations at large-modulation index levels. Such behavior was explained as repeated doubling of the period of the response until it becomes long enough that it appears to show no period at all. Experimental studies of the laser behavior, however, indicated that only a few period-doubling bifurcations were observed. On the basis of this difference, the theoretical models were revised and new terms were included in the rate equations.

Chaotic behavior was observed for the first time in a modulated laser diode from a 1.55-µm distributed-feedback (DFB) laser when a large modulation index was applied.⁶ A unique sequence of irregular behavior also was observed in which period doubling, period quadrupling, and period tripling stages preceded a regime that was suspected to correspond to deterministic chaos. Very recently, the same experiment on multiple-quantum-well laser diodes has produced the sequence of period doubling followed by period tripling, but no chaos has been observed.⁷

Now, we must stress two important facts. The first is that the sequence of periodic regimes prior to chaotic behavior is significant. Only three different mechanisms, known as routes to chaos, have been identified for the appearance of deterministic chaos in nonlinear systems. The fact that none of them accounts for the observed route to chaos in directly modulated laser diodes poses the question as to which kind of dynamics underlies the appearance of chaos in the experimental setup. Attention should be paid to this, since the answer also could account for the difficulties in observing the theoretically predicted route to chaos.

The second fact is that chaotic behavior could only be "suspected." It is important to take into account that in experimental setups, the information on which the researcher relies to determine the type of behavior is the output power spectra of the device. Due to the frequencies involved in fiberoptic communications—on the order of several GHz—it is difficult to apply nonlinear techniques, such as periodic sampling of output, at the modulation rate. The problem arises when one wishes to distinguish in an experimental setup a chaotic regime from random noise, which is present in every real observation due to the numerous noise sources. In the system's output, chaos induces a wide band of frequency components, as would colored noise. Hence, much effort has been made to distinguish noise from chaos, ranging from measuring dimensions of the time series to singular value decomposition.

Consequently, it has become crucial for theoretical studies to simulate the experimental measuring procedure and establish similarities between the two. Once the similarities are obtained, one can apply all of the resources of bifurcation theory to investigate the origins of the different dynamics.

A key factor: random noise fluctuations
When the behavior of the laser is investigated as a function of the modulation amplitude, m, using the rate-equation description for the laser diode in which Langevin sources introduce the random noise terms, the regimes at different levels can be represented (see Fig. 1). Here, we simulated the experimental observations by averaging the Fourier transform (through an FFT algorithm) of several time series for each modulation level. In each graph of the figure, the arrow at f_m locates the frequency of the direct current modulation. Additional peaks can be observed in these graphs and their location is used as an indication of the dynamics of the laser for that particular modulation level.

As the modulation index increases, we observe a period quadrupling stage at m = 4.2 (with peak at f_m/4 and higher harmonics), period tripling at m = 9.8 and m = 10.4 (with lowest frequency peak at f_m/3) and a regime with a wide band of frequency components at m = 11.2. The first thing we can point out is that the graphs in the figure agree well with the experimental results, theoretically reporting the sequence of period quadrupling, period tripling, and chaos observed experimentally. The period tripling stage at m = 10.4 shows the experimentally observed bat-shaped profile. This profile, which appears to result from merging the spectra at m = 11.2 and m = 9.8 is indeed a modulation level at which a chaos and period tripling coexist and show up simultaneously. The coexistence of these regimes can account for the absence of the chaotic regimes in experimental observation, where it has been instead interpreted as a periodic behavior.

The first fact we can highlight is that the random sources allow us to break the principle of uniqueness of solution. However, implicit in the reasoning we are using is the fact that the spectra profile for m = 11.2 corresponds undoubtedly to chaos. Why is this broad band not produced by the noise sources as well, as indicated in the previous section? For that purpose, bifurcation theory can be applied, and instead of representing experimentally available data, we can use the state-space representation, making use of the numerical data.

The diode laser's state-space representation plots the photon and carrier densities, sampled at time intervals that are integer multiples of the modulation period (see Fig. 2). Although the samples occupy a large area (indication of chaos), these are distributed over a definite structure (which eliminates the random origin). These samples are shown to embed the period tripling behavior, shown with dark circles. This is the structure over which the samples arrange themselves, determined by the unstable solutions that are responsible for many important characteristics of the nonlinear systems.⁸ In Figure 2, the red square corresponds to an unstable solution embedded into the area occupied by the samples of the observed dynamics. These unstable solutions can give rise to sudden drops of the output intensity of the laser, as has been recently reported.⁹ The use of nonlinear dynamics to provide an understanding of the dynamics of chaos has enabled new control procedures to be devised that can then be used to produce secure coding of transmitted information. For more information on the subject, a helpful book about nonlinear dynamics is Dynamics of Lasers, by C. O. Weiss and R. Vilaseca.

REFERENCES

1. Lasher, Solid State Electron. (Oct. 1964).
2. Goldstein and Welch, Proc. IEEE (June 1964).
3. H. Statz and G. deMars, Quant. Elect. (Columbia Univ. Press, 1960. C.H.Townes Ed.).
4. G. P. Agrawal, Fiber-optic Communication Systems (Wiley, 1992).
5. F. T. Arecchi et al., Phys. Rev. Lett. 49, 1217 (1982).
6. H. F. Liu and W. F. Ngai, IEEE J. Quant. Electron. 29, 1668 (June 1993).
7. S. Bennett, C. M. Snowden and S. Iezekiel, IEEE J. Quant. Electron. 33, 2076 (Nov. 1997).
8. H. Lamela, G. Carpintero and P. Acedo, IEEE J. Quant. Electron. 34, 491 (1998).
9. G. Carpintero and H. Lamela, Proc. SPIE 3944 (January 2000).

Dr. GUILLERMO CARPINTERO is this year's recipient of PennWell's Heather Williamson Messenger Young Investigator Award. He is with the optoelectronics and laser technology group headed by Dr. HORACIO LAMELA at the Universidad Carlos III de Madrid, Av. de la Universidad, 30. Leganés 28911, Madrid, Spain; e-mail: [email protected] and [email protected]