Rich and varied
The silica glass found in optical fibers is perhaps the last material one might think to choose to generate nonlinear optical effects. The symmetry properties of silica rule out the occurrence of second-order nonlinear processes, and the coefficients for third-order effects are at least 100 times smaller than coefficients in conventional nonlinear optical materials. Nevertheless the intensities that result for even modest input powers confined in micron-sized fiber cores are great enough to activate a surprising variety of nonlinear effects.
Because a signal in modern optical fiber attenuates only about 5% per kilometer at 1550 nm, nonlinear effects can accumulate over great distances. As might be expected, this can be a problem in optical networking, particularly for wavelength-division multiplexing (WDM). The difficulties caused by stimulated Brillouin scattering, stimulated Raman scattering, and four-wave mixing—and methods for coping with them—will be discussed in the final article in this series.
Other nonlinear phenomena in optical fiber are rich and varied. Self-phase modulation (SPM), particularly when combined with group velocity dispersion (GVD), is especially effective in generating nonlinear phenomena for ultrafast (picosecond and shorter) pulses. The combination can be used to produce soliton pulses, for example. In a different arrangement, the combined effects can be used to compress the duration of optical pulses.
Fundamentally nonlinear
Self-phase modulation arises when an ultrafast pulse travels though a point in the fiber, increasing the local index of refraction. The center of the pulse, which of course is more intense, experiences a larger index of refraction than the leading and trailing edges. The wavelengths at the front of the pulse are red-shifted, while the trailing edge wavelengths are blue-shifted. Such a pulse is said to be chirped.
Group velocity dispersion is the result of different Fourier components of a pulse traveling at different phase velocities. The optical path length of different wavelengths varies, either because an optical material actually disperses the wavelengths, or because the wavelength components are separated and made to travel different paths before being recombined. In normal GVD the longer wavelength pulse components travel faster than the shorter. In anomalous GVD, shorter wavelengths travel faster than longer ones.
It should be noted that networking engineers tend to prefer a different definition of group dispersion, called group delay dispersion, or GDD. Group delay dispersion is measured in units different from GVD, and the sign of GVD is reversed from GDD. Group delay dispersion has the practical advantage of giving the value that a pulse broadens over a given distance.
Short and shorter
Both SPM and GVD can be used together in single-mode fibers to compress ultrafast pulses via two general techniques. The grating-fiber method is used in the visible and near-infrared regions. The soliton-effect compressor is used for wavelengths typical of networking applications, between 1.3 and 1.6 µm. Each technique can be implemented in a variety of ways.
In a grating-fiber compressor, the wavelength of the input pulse falls in the normal dispersion regime of the fiber, which imposes a chirp on the pulse through SPM. The resulting pulse can have its spectral width increased by a factor between, say, 3 and 5. The chirped pulse is then passed through an external pair of gratings, which are designed to produce anomalous GVD (see Fig. 1).
By making the optical path length of the longer wavelengths substantially greater than the path for the shorter wavelengths, the trailing edge of the pulse catches up to the leading edge, and the pulse can be compressed to less than its initial value. Having the pulse double-pass the grating doubles the dispersive power, and also serves to restore the beam to its original cross section. A fiber grating can also be used to produce the anomalous GVD, resulting in a compact, all-fiber design.
Chirped pulse amplification (CPA) can also be accomplished in an all-fiber scheme. This technique prevents amplified peak powers from reaching the damage threshold for optical components by amplifying a pulse after it is first chirped and stretched in duration, then recompressing it. A modelocked fiber laser seeding an all-fiber stretcher and compressor, together with a fiber amplifier, is a robust and compact system that can produce femtosecond pulses at repetition rates of hundreds of kilohertz.
Basically solitary
To discuss the soliton-effect compressor, one should realize that, in a sense, soliton behavior is a natural mode of propagation in a silica fiber in which anomalous dispersion is commonplace. Anomalous dispersion occurs near an absorption band in a material, at the center of which dispersion is zero. Ordinary silica fiber has zero dispersion at about 1.31 µm, but modern fiber is often engineered so that zero dispersion is shifted to different wavelengths for a variety of purposes.
Transmission in the presence of anomalous dispersion is inherently prone to the production of nonlinear effects. The propagation of a continuous-wave beam is unstable in the anomalous regime, for example, because it will readily break up into a train of pulses. Under the right input conditions, pulses will also display soliton-like behavior in the presence of anomalous dispersion.
The soliton-effect compressor consists simply of a single piece of fiber of the proper length. The input pulse has a wavelength that falls in the anomalous GVD regime of the material. Compression occurs because the pulse experiences the soliton-like effect of narrowing in phase before its input shape is restored over a periodic distance in the fiber.
Making the ordinary exotic
Ultrafast pulses can induce nonlinear effects in otherwise ordinary fiberoptic components. A variety of these components are being investigated as possible control devices for a next-generation all-optical network. A few examples follow.
Couplers are commonly used to transfer a signal from one fiber to another. As power increases in the input fiber, SPM detunes the mode relative to the second fiber core, defeating the evanescent wave effect that otherwise transfers the signal to the second fiber. In principle, this mechanism could form the basis of an all-optical switch.
Different types of fiber interferometers, such as the Mach-Zender interferometer (MZI), create interference between two or more waves in the fiber to form modulators, pulse shapers, filters, and switches. Interference for intense pulses is often caused by cross-phase modulation (XPM), similar to SPM except that the phase modulation is produced by a separate intense wave. The XPM created by control pulses can shift the phase of the signal pulses, creating an all-optical gate by causing the signal to reflect or transmit through the interferometer.
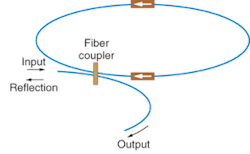
A fiber interferometer can also be operated as a mirror that selectively transmits different power levels by making use of phase modulation. Because the nonlinear phase shift depends on the intensity profile, the central portions of intense pulses in a Sagnac interferometer can be made to interfere constructively while the lower power wings are left to interfere destructively. Such an arrangement can be used like a saturable absorber for modelocking that operates at femtosecond levels.
Still another nonlinear phenomenon that can take place in a Sagnac fiber interferometer is the generation of "squeezed states" (see Fig. 2). An optical pulse in a squeezed state has a noise level within a given frequency range that is reduced below even the quantum limit for random amplitude fluctuations. As might be expected, a fully quantum-mechanical explanation is needed to account for this phenomenon. A variety of nonlinear optical processes, principally four-wave mixing, act to reduce the noise level of the signal pulse.
Holey promise
Diffraction gratings are ubiquitous in optical networks and serve several purposes. Grating structures fabricated in the fiber, such as fiber Bragg gratings, can also produce anomalous dispersion. This is true even if the grating itself is made from material that has normal dispersion at the signal wavelength.
A fiber grating reflects light not only at the exact Bragg wavelength but at a band around it. This is referred to as the stop band or the photonic bandgap in analogy to the transmission of electrons in the presence of a semiconductor bandgap. At wavelengths close to its bandgap, the optical dispersion of a grating can be very large. A grating 10 cm in length, for example, can cancel the material dispersion accumulated by a pulse traversing 50 km of fiber.
This concept of a photonic bandgap is extended to more than one dimension in so-called holey fibers. Holey fiber contains microscopic air holes in a more-or-less regular array that run the length of the fiber (see photo, p. 82). There are different types of holey or microstructure fiber, depending on whether light is transmitted through the glass rather than through the air spaces (see Laser Focus World, May 2003, p. 99).
Photonic crystal fiber, which transmits light through the air space, illustrates the bandgap effect. Here the refractive indices of the fiber are reversed from the requirements of total internal reflection, as used in conventional fiber. These fibers rely on the photonic bandgap of the surrounding grating-like structure to confine the light.
In terms of nonlinear effects, the dispersion in holey fibers can be much greater and adjusted over a broader spectral range than is possible in conventional fiber. The wavelength for zero dispersion in such a fiber has been reduced to as low as to 550 nm, and such fibers can produce solitons at visible wavelengths. The development of holey fibers at this time is reminiscent of the development of optical fiber itself in its infancy.
Next month's article will discuss fiber systems.