Forward-error correction can enhance transmission capacity

Forward-error correction relies on mathematical coding to detect and correct errors in a stream of data. Coding circuits in the transmitter add extra bits to the data stream, which are analyzed by coding circuits in the receiver to detect and correct errors arising from transmission. The resulting reduction in bit-error rate adds extra margin to system performance at the cost of transmitting additional overhead bits and buying extra electronics for the transmitter and receiver.
Error detection and correction techniques were first applied to computer data storage and transmission. Fiberoptic developers began to use error correction in the early 1990s to enhance performance of long-haul submarine cables. Although error correction adds to system costs, that premium has proven worthwhile because reducing error rates at low receiver powers can significantly stretch transmission distances, and applications are expanding to other long-haul systems.
Limits on fiber error rates
Bit-error rate is a key figure of merit for fiberoptic system performance, so anything that reduces it can pay important benefits. The specific target depends on the application; typically telecommunications systems look for an error rate of no more than 10-12 or one error per trillion received bits.
The raw bit-error rate depends on the electronic signal-to-noise ratio at the decision circuits. In a system carrying one optical channel, the signal-to-noise ratio depends largely on receiver power and sensitivity. The raw error rate increases rapidly as received power drops but because the noise comes from shot noise, amplifier noise, and thermal noise, increasing signal power can reduce the error rate (see Fig. 1).
Wavelength-division multiplexing adds crosstalk noise, which cannot be reduced simply by turning up the power. Some interchannel crosstalk is inevitable because optical filtering is imperfect. Nonlinear effects also cause crosstalk, and in that case increasing the optical power multiplies the strength of the nonlinear effects and of the noise they generate. Efforts to mitigate the effects of crosstalk noise pushed fiber-system developers to consider forward-error correction.
Error detection and correction
An error detection and correction code operates on a block of data. Its power depends on both the number of bits added to the block and the power of the mathematical code. The simplest task is to detect that an error has occurred; it is harder to identify the incorrect bit and correct it. All codes have limited capacity, so large numbers of errors can block transmission.
Parity checking is a simple code that adds a parity bit to an eight-bit byte. The transmitter adds the data bits to determine if their sum is odd or even. Then the circuit adds another bit to give the desired parity. If the sum of the data bits is even and the parity is odd, it adds one bit to make the sum odd. At the other end, the receiver adds all nine bits to see if the sum matches the parity. If the sum and parity do not match-for example, the sum is even and the parity is odd-then the receiver knows the byte contains an error. Parity checking alone cannot identify which bit is incorrect, so the receiver requests retransmission of the entire byte. Parity checking also cannot spot a pair of errors, because it verifies only whether the sum is even or odd.
Cyclic redundancy checking can spot more errors in larger blocks of data. It treats the entire block as a number, which is divided by a suitable quantity, giving a quotient (which is thrown away), and a remainder, which is appended to the data block at the transmitter. The process is repeated at the receiver where the new remainder is compared to the one sent with the data block. If they don't match, the receiver requests retransmission of the data block.
Forward-error-correction codes identify which bits are wrong and correct them, avoiding time-consuming retransmission, and better matching the requirements of telecommunications systems. A simple example is redundant retransmission, which sends every data bit three times and compares the results. If two bits are zero and the third is one, the receiver assumes that the transmitter originally sent a zero, effectively correcting the result. That code is not practical because it triples the data rate, but it illustrates coding principles. The code is identified by a pair of numbers (n, k), where n is the total number of bits in the block and k is the number of data bits. That makes the redundant code a (3, 1) code. The smaller the number of added bits (n-k), the more efficient the code. Efficiency is measured by calculating the overhead ratio, (n-k)/k, which is 200% for the (3, 1) code.
Practical error correction
The efficiency of error correction generally increases with the size of the coded blocks. Mathematical coding allows a limited number of added bits to detect and correct errors in a much larger block, reducing the overhead while allowing correction of multiple errors. With blocks of hundreds or thousands of bits, overhead can be reduced from 7% to 25%. The error-correction codes usually used in fiberoptic systems are Reed Solomon codes, in which a polynomial derived from coding theory is divided into the data bits, and the remainder is used as the check bits. This code is called cyclic because the calculation can be done by rotating the bits cyclically through shift registers.
Reed Solomon codes organize transmitted data in the form of symbols, each containing m bits, which in turn are grouped into blocks containing 2m-1 symbols or m(2m-1) bits. This includes both data bits and check bits. Thus a Reed Solomon code for 8-bit bytes would contain 255 bytes (symbols) or 2040 bits. That code can correct errors in up to half as many symbols (in this case, bytes) as are added. Thus, a (255, 239) Reed Solomon code, which contains 16 check bytes, can correct errors in up to 8 of the 239 data bytes transmitted. In practice, the 239 data bytes include 238 bytes of user data and one framing byte generated at the transmitter.
Submarine cable systems adapted the (255, 239) Reed Solomon code in the early 1990s, because chips were readily available, and it remains widely used. The low 6.3% overhead makes that code attractive, so transmitting 10 Gbit/s of user data requires a line rate of only 10.7 Gbit/s. The International Telecommunications Union has also standardized (255, 223) code, which has about 13% overhead and can correct up to 16 byte errors.Dramatic improvement
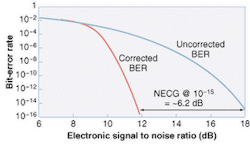
In essence, error correction reduces the signal-to-noise ratio required to achieve a bit-error rate by a quantity called the net effective code gain (NECG), which is measured in decibels. Forward-error correction with a (255, 239) Reed Solomon code, for example, makes it possible to achieve a bit-error rate of 10-15 with a signal-to-noise ratio 6 dB less than would be required without correction (see Fig. 2). This also can be considered to be reducing the raw bit-error rate from about 10-4 to a corrected rate of 10-15.Further refinements are possible. Standard error correction assumes that errors are scattered randomly through the bit stream, but in practice they may be clustered. Noise from a short-term peak in polarization-mode dispersion, for example, can cause a cluster of errors that could overwhelm normal forward-error correction. One way to overcome this is by interleaving or time-shifting the data stream to spread the errors out (see Fig. 3). In this example, incoming data blocks are broken up, so the first bit in each byte is transmitted in one block, the second bit in another block, and so on. Then the original data blocks are reassembled at the receiver. In that way, a sequence of 40 consecutive incorrect bits would be divided, putting five into each of eight consecutive data blocks, a level that can be corrected.
The power of interleaving can be increased by concatenating two successive layers of error-correction codes. Incoming blocks first go through conventional forward-error coding, then that coded signal is interleaved and a second level of error-correction coding is added before transmission. At the receiver, the data first passes through the second level of error correction, which can handle scattered errors but not large bursts of closely spaced errors. De- interleaving returns the partly corrected bits to their original sequence, scattering any remaining transmission errors through a larger number of blocks, so these residual errors can be corrected.
Outlook for error correction
Other coding techniques offer stronger error correction, although with some tradeoffs. Turbo convolutional codes treat user data as a matrix and add separate check bits to the rows and to the columns, so each can be checked individually for errors. This two-level checking comes at the cost of higher overhead, and does not work well in systems that require 10-15 bit-error rates. It can, however, offer significant improvements for applications where a 10-7 error rate is acceptable.
Other techniques also are in development, such as "soft decision" sampling at the receiver, which uses 2 or 3 bits of analog resolution rather than a binary decision circuit. Two-bit codes can reduce the required signal-to-noise ratio by about 1.5 dB margin, and adding a third bit adds a few tenths of a decibel more. New codes also are in development, although current ones are approaching theoretical limits.
The complex processing required limits the speeds of current error-detection chips. In practice, most chips have ports operating near 622 Mbit/s, and internally split that signal among several parallel circuits operating near 100 Mbit/s. Higher-speed signals are demultiplexed down to 622 Mbit/s for coding and decoding. This may sound cumbersome, but the economics of chip production make it the most practical approach.
Today, powerful forward-error correction is standard in long-haul submarine systems, which push performance limits. Development of a standard based on the (255, 239) Reed Solomon code has led to its use in some long-haul terrestrial systems spanning 600 km or more. Applications are likely to continue growing as systems move to higher data rates and longer transmission distances, stressing performance limits.
ACKNOWLEDGMENT
Thanks to Frank Kerfoot, Tyco Submarine Systems, for an outstanding tutorial at OFC 2002 and for his patience with my questions.
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.