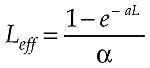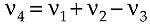Mitigating nonlinear effects is essential to long-haul transmission systems
Nonlinear effects can impose significant performance limitations on fiberoptic systems. Although glass itself is a highly linear material, fiberoptic transmission pushes nonlinear thresholds in two important ways. First, fiber geometry strongly concentrates optical power in the core of single-mode fibers, producing the high power densities that foster nonlinear effects. Second, fiberoptic transmission requires sending signals through kilometers of fiber, and nonlinear effects are proportional to distance.
Fiber nonlinearities manifest themselves primarily as noise and distortion. Noise includes crosstalk such as the spurious signals produced by four-wave mixing, as well as distortion of the signals themselves. In order to understand how to control and limit these nonlinearities, we need to start by looking at their nature.
Defining nonlinearity
Linear interactions are called linear because they are proportional to the first power of the incident electric or magnetic field. Simple absorption is a good example of a linear interaction; the amount of light absorbed is linearly proportional to the lightwave amplitude. Nonlinear interactions are proportional to higher powers of the lightwave amplitude, so their strength increases more rapidly as the optical power increases.
The wave amplitudes are not the total power but the power density or irradiance, power per unit area or watts per square centimeter. Although the peak optical power in a fiber is typically measured in milliwatts, this power is concentrated in a small area in the core of a single-mode fiber, so the power density is measured in kilowatts per square centimeter. Because the intensity is not distributed uniformly through the core, peak power densities can exceed a megawatt per square centimeter.
The strength of a nonlinear effect is also proportional to the nonlinear coefficient of the host material (glass in an optical fiber) and the total distance light travels through the material at that power. Although the nonlinear coefficients of glass are small, the cumulative nonlinear effects of fiber transmission are increased by the appropriate multiple of the power density (the square for a second-order nonlinearity) and a factor that accounts for the total transmission distance. The magnitude of nonlinear effects does not increase linearly with distance because attenuation decreases the optical power level, effectively reducing the length of the fiber span. Thus, the impact of nonlinear effects actually depends on a quantity called effective length, defined as:where L is the total length of the fiber span and α is the attenuation in units of inverse kilometers. Therefore, the effective length of a fiber span with typical attenuation of 0.22 dB/km is about 20 km, although the actual length of fiber between optical amplifiers (or between transmitter and receiver) is considerably longer. In a system with optical amplifiers, the total nonlinearity is the sum of the effective lengths of all fiber spans between transmitter and receiver.
Types of nonlinearities
Several nonlinear effects can occur in fiberoptic systems transmitting milliwatts or more per channel.
Stimulated Brillouin scattering arises when light generates acoustic waves along the length of the fiber, producing variations in refractive index that scatter light back in the direction from which it came, increasing signal attenuation. The process can occur when the fiber carries only a single optical channel, which it shifts by 11 GHz when it scatters the light. The threshold for stimulated Brillouin scattering is several milliwatts in a standard step-index single-mode fiber; it can be raised by broadening the laser output spectrum. Nonetheless, stimulated Brillouin scattering is strong enough that it can limit usable optical power to about 10 mW per channel.
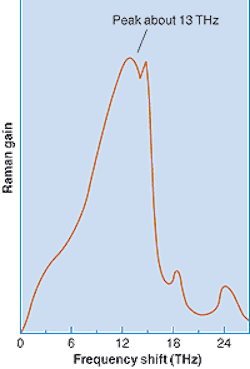
Stimulated Raman scattering is the absorption of a photon by an atom in a solid that uses part of the energy to excite a vibrational energy mode and releases the rest of the energy as a second, longer-wavelength photon. The Raman scattering process shifts the wavelength by a characteristic amount for each material (see Fig. 1). Strictly speaking, stimulated Raman scattering is the transfer of energy from the shorter-wavelength pump signal to a second channel that is present at a longer wavelength. Spontaneous Raman scattering occurs when noise causes the scattering. The process can both reduce strength of a signal at the shorter wavelength and produce noise at the longer wavelength. (The same process transfers energy from a pump wavelength to amplify a longer wavelength in a Raman amplifier.)
Four-wave mixing is the interaction of three waves passing through a fiber to produce a fourth wave at a frequency equal to the sum of the frequencies of two waves minus the frequency of the third:Self-phase modulation arises because refractive index varies with light intensity, and thus varies as intensity changes during a pulse. This causes the intensity modulation of a single optical channel to modulate the phase of the signal at that wavelength. This phase shift accumulates along a fiber, broadening the range of wavelengths in the signal, and increasing the impact of chromatic dispersion. If the chromatic dispersion is negative (or "anomalous"), that chromatic dispersion can combine with self-phase modulation to produce soliton pulses that retain their shape as long as they have sufficient intensity.
Modulation instability can arise in regions of anomalous dispersion if the interaction between dispersion and self-phase modulation becomes unstable. It introduces noise by causing pulses to break up.
Cross-phase modulation is the cross-channel version of self-phase modulationintensity modulation of one channel causes refractive-index variations that induce phase modulation of other channels. It increases as the number of channels increases and the spacing between channels decreases.
Mitigating nonlinear effects
The most straightforward way to mitigate nonlinear effects is to keep power densities below the threshold at which they become significant. Attenuation reduces power level along the fiber, so power density need only be reduced in the zones in which power is highest, near to the transmitters or optical amplifiers.One approach is to install single-mode fibers with large effective area near the transmitters to reduce power density by spreading the power through a larger volume. Although large-effective-area fibers may only halve the power density, that can be a significant advantage when they are used in the first 10 or 20 km of a fiber span, where power is highest. Smaller-core fibers can be used where power is lower, to balance other transmission properties such as dispersion slope in WDM systems.
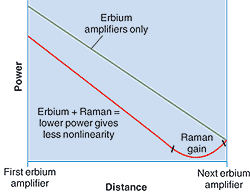
Peak power in a span also can be reduced by distributing some gain in Raman amplification stages rather than concentrating it entirely in lumped erbium-doped fiber amplifiers. Raman amplification can be distributed in parts of the transmission fiber where power levels are low, reducing the power levels required at the exits of transmitters or amplifiers (see Fig. 3).
Reducing amplifier spacing is another alternative with similar goals. In long-haul systems it can cause higher costs and increase noise levels, but it's acceptable in shorter metro systems in which nonlinear effects have less distance to build up than in long-haul networks.Increasing data rates can increase nonlinear effects because they reduce bit intervals, leaving less time for the detector to receive the number of photons it needs to detect a bit. Multiplying the data rate by four, for example, leaves only one-quarter the time to deliver the required number of photons, forcing a four-fold increase in average power at the receiver. That 6-dB increase can cross the threshold for nonlinear effects.
Dispersion management is required to control four-wave mixing. When a fiber has zero dispersion, pulses stay in phase over long distances, creating the ideal situation for four-wave mixing to accumulate. Nonzero dispersion causes the channels to drift out of phase, reducing the accumulation of four-wave mixing crosstalk (see Fig. 4). To achieve the low total dispersion needed for high bandwidth, designers can concatenate two or more types of fiber with different dispersion characteristics that offset each other. Each segment of fiber thus has the high local dispersion needed to prevent four-wave mixing, but the combination of different fibers gives the low total dispersion needed for high bandwidth.
Dispersion management raises other potential nonlinear problems because special dispersion-compensating fibers have small cores, which makes them particularly vulnerable to nonlinear effects. These side effects can be limited by using dispersion-compensating fiber only where powers are low, by selecting different types of transmission fiber to balance dispersion, or by using other techniques such as transmission in higher-order modes.
Future prospects
Continuing research promises new approaches to control nonlinear effects. Phase or frequency modulation, for example, could avoid effects arising from intensity modulation of the signal. That possibility has renewed research interest in coherent transmission and differential phase-shift keying, which were abandoned in favor of WDM.
Ultimately, there may be no way to avoid nonlinearities. "Once you go a long distance, things start adding up and something happens eventually," says Govind Agrawal, a specialist in nonlinear fiber optics at the University of Rochester (Rochester, NY). Limiting power levels inevitably limits transmission distances or data rates. The only real way to fix nonlinearities may be full-scale three-R regeneration of the signal before it's overwhelmed by noise (see Laser Focus World, April 2002, p. 75).
FURTHER READING
1. G. P. Agrawal, Nonlinear Fiber Optics 3rd ed. (Academic Press; 2000).
2. J. A. Buck, "Nonlinear effects in optical fibers," Chapter 3 in Michael Bass ed., Handbook of Optics Vol. 4 Fiber Optics and Nonlinear Optics (McGraw-Hill, NY; 2001).
About the Author
Jeff Hecht
Contributing Editor
Jeff Hecht is a regular contributing editor to Laser Focus World and has been covering the laser industry for 35 years. A prolific book author, Jeff's published works include “Understanding Fiber Optics,” “Understanding Lasers,” “The Laser Guidebook,” and “Beam Weapons: The Next Arms Race.” He also has written books on the histories of lasers and fiber optics, including “City of Light: The Story of Fiber Optics,” and “Beam: The Race to Make the Laser.” Find out more at jeffhecht.com.