Long distance distribution of quantum keys
Considered a promising technology, quantum communication (QC) is significantly different from conventional communication. Specifically, traditional telecommunications are not technically bound to a region. Signals travel around the world in milliseconds, without users recognizing if the server is on one continent or another. Simply put, signal distribution and amplification are everywhere.
With QC, there is most often a source of entangled photon pairs. These photons are sent directly to two receivers. A sequence of such single photons serves as a key for subsequent encryption of the actual message, transferred on classical channels. This concept is called quantum key distribution (QKD). The source of the photons can be right beside one of the receivers, or far away. The distribution of such signals through optical fibers is limited to a few hundred kilometers at best as the photons get absorbed in the fiber. Amplifiers are not allowed.
This article reviews a recently proposed constellation where the source of entangled photons is on a satellite, sending entangled photons to two ground stations. This is a first step for long haul connections, limited to the free line of sight. For a truly global network, a chain of satellites and a technique of storing the quantum information—the so-called quantum memories—is necessary.
What is so special in quantum communication?
QC uses a sequence of single photons to generate a secret key for encryption. In a common scheme it uses entangled photon pairs, specifically two photons with a fixed relation of parameters such as frequency (that is, color), polarization, or amplitude. For example, the entangled photons could have perpendicular polarization states and thus measuring one of the entangled photons may reveal the polarization of the other. By comparing the measurements on each side, it is possible to generate and share a secret key between the users.
Eavesdropping is excluded as reading the photon destroys the entanglement, which can be measured before using the generated keys. This is referred to as measurable security, which also eliminates amplification since one cannot create multiple copies from the one photon carrying quantum information without determining that information.
The generation of entangled photons has been demonstrated in many labs, in mobile applications and also in space. One way is a nonlinear process where one blue photon is converted into two red photons. Measuring the state of a single photon is state of the art, although some effort has to be taken to limit the noise on the detected signal.
The actual challenge is in the transport of single photons. Even the best optical fibers show losses—and again, no amplification is possible. Absorption is an exponential effect that limits the transmission over optical fibers to ranges much smaller than 1000 km.
Satellites for quantum key distribution
One way to get QC over longer distances is the free space transmission via satellite. This replaces exponential attenuation with mostly diffractive losses, which is governed by a 1/x2 function. And still, the signals have to cross the atmosphere at least two times, which adds attenuation. The wavefront distortion can be compensated in the ground-based telescopes using the tricks of modern astronomy.
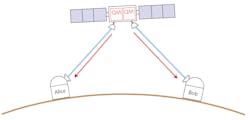
Considering satellite-based QC requires elimination of another dogma. In classical telecommunications, information is sent from point 1 to point 2. In QC, a source of entangled photons S is placed on a satellite, sending photons to ground stations Alice and Bob (see Fig. 1). A sequence of such signals forms a secret key, which is received at Alice and in a related form at Bob. QC in this sense is not the transmission of a message, but the generation and distribution of a secret key for encryption.
This has been done experimentally with the Chinese MICIUS satellite already, where distant ground stations with sophisticated telescopes received entangled photons from the satellite. Although losses are much smaller than with a comparable fiber connection, the absorption and diffraction processes still lead to a signal with interruptions. Generation of photons at megahertz rates at the source usually leads to a quantum signal at the receiver in the order of a few hertz or less.
Once a longer stream of photons has been received, it can be used to encrypt a regular communication and sent via regular networks. As such, the actual message is sent on regular speed after encryption, while the key has been transmitted at rates of less than a photon per second.
Sending over the horizon
This setup does not enable going beyond the horizon of the satellite. Theoretically, it can address half of the earth. Yet, in real world experiments, the horizon is about 2000 km away for satellites in the low Earth orbit. A longer line requires intermediate nodes—a concept that is also crucial for distributed structures of quantum computing. And again, the solution requires thinking off the beaten tracks of telecommunication.
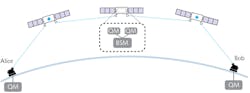
The sketch in Figure 2 explains the concepts: Two satellites create entangled pairs of photons each. These photons are received by communicating parties on the ground and the central satellite receives signals from both satellites. The entanglement is then transferred across larger distances via entanglement swapping.1 This operation requires the simultaneous detection of photons from two paths. The states are measured at B, and the result is transferred through conventional lines to ground stations A and C. There, the results from the incoming photons and from B are connected, leading to valid results of the extended or swapped entanglement. A and C then share a key code.However, given the probabilistic nature of entanglement generation and the lossy communication channel, the simultaneity condition for photon measurements at the middle satellite B is extremely difficult to satisfy. Thus, if one has quantum memories, then the incoming photons can be stored in two memories and recalled on-demand when both photons arrive. This would also allow to compensate for different runtimes due to different path lengths. In the end, a solution with quantum memory enhances the generated key rate significantly and allows one to realize more complicated architectures that involve many quantum nodes.
Storing quantum information
Quantum memory (QM) is quite different from an electronic memory. The storage medium for QM is an atom, or an ensemble of atoms. QC is based on photons and thus, the QM has to transfer a specific property (degree of freedom) from the photon to the atom. It should be possible to map this particular property back into a photon.
For such a quantum memory, several ideas were developed and explained elsewhere.2 Amongst others, it uses atoms in warm or cold gases, or rare-earth ions in certain crystals. It could be single atoms or groups of atoms, or even single electron spins.
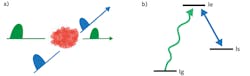
A major process for QM is reminiscent of basic laser physics (see Fig. 3): the photon is absorbed by an atom with three levels. In a simple picture, the absorption moves the electron from the ground level g to the excited level e. Then a laser pulse moves the electron to the level s, which is not allowed to relax to the ground level. To restore the photon, the same laser radiation is used to raise the electron from the storage level s to the level e, and by relaxing to the ground state g, it emits a photon that carries the properties of the original photon.Cold and warm gases for quantum memory
Such a process is not trivial. A single atom or an ensemble of atoms has to be hit by a single photon and subsequently by a defined laser pulse. Such techniques have been developed and tested with several different systems, including ultracold atoms—so-called Bose-Einstein condensates (BECs)—which have already been brought to space. Step by step, the technology was advanced until it was demonstrated on sounding rocket3 and finally arrived at the International Space Station (ISS) in 2018.4
Next-generation atomic physics experiments using warm vapors will use palm-sized setups. Scientists from Humboldt University of Berlin (HU Berlin; Germany), Ferdinand-Braun-Institut (FBH; Berlin, Germany), and the National University of Singapore (NUS), supported by the German Space Agency (DLR) and Berlin University Alliance, have developed a system which is that small already (see Fig. 4).5 This module contains a distributed feedback (DFB) laser module and a cell for warm atom experiments, which is currently being adapted for storage experiments.A global quantum network
Researchers suggest a new system to put the pieces together for a satellite based long-haul connection for QC.6 Based on a network of satellites, it would replace the exponential attenuation of ground-based connections by diffractive losses, which are governed by an inverse square law. The new approach with a chain of satellites would overcome the line-of-sight limitation between satellite terminals and ground stations.
The actual benchmark for such a solution is the entanglement distribution rate across the communicating parties—that is, the rate with which entangled photons are successfully transmitted to the final ground stations. Now, extensive simulations show that a chain of satellites equipped with quantum memories can be three orders of magnitude faster in entanglement distribution over global distances than existing protocols relying on quantum memories on ground stations.7
Outlook
Globally, feasible QC will likely require satellite links. This assumes remote operation of the sources of entangled photons as well as quantum memories. While the first has already been demonstrated in space, the latter still requires research and development. Ensembles of atoms are excellent candidates for quantum memories. The technology for such experiments is, for example, flying on the ISS already. Recent simulations show that once the memories are established, they will allow the distribution of quantum keys with higher entanglement rates than comparable ground-based networks.
REFERENCES
1. See https://bit.ly/3nppUyO.
2. M. Afzelius, N. Gisin, and H. de Riedmatten, Phys. Today, 68 (2015); http://dx.doi.org/10.1063/pt.3.3021.
3. M. D. Lachmann et al., Nat. Commun., 12, 1317 (2021)
4. E. Elliott, M. Krutzik, J. Williams, R. Thompson, and D. Aveline, Microgravity, 4, 16 (2018).
5. A. Strangfeld et al., J. Opt. Soc. Am. B, 38, 1885–1891 (2021).
6. M. Gündoğan et al., Quantum Inf. (2021); https://doi.org/10.1038/s41534-021-00460-9.
7. C. Simon, Nat. Photonics, 11, 678 (2017); https://www.nature.com/articles/s41566-017-0032-0.
About the Author
Andreas Thoss
Contributing Editor, Germany
Andreas Thoss is the Managing Director of THOSS Media (Berlin) and has many years of experience in photonics-related research, publishing, marketing, and public relations. He worked with John Wiley & Sons until 2010, when he founded THOSS Media. In 2012, he founded the scientific journal Advanced Optical Technologies. His university research focused on ultrashort and ultra-intense laser pulses, and he holds several patents.
Markus Krutzik
Group Leader, Optical Metrology Group at Humboldt-Universität zu Berlin
Markus Krutzik is a group leader of the Optical Metrology Group at Humboldt-Universität zu Berlin (Berlin, Germany).
Mustafa Gündoğan
Marie Skłodowska-Curie Research Fellow, Humboldt University of Berlin
Mustafa Gündoğan is a Marie Skłodowska-Curie Research Fellow at Humboldt University of Berlin (Germany).