Lossless Image Compression Example

For storage and transmission of large image files it is desirable to reduce the file size.

For consumer-grade images this is achieved by lossy image compression when image details not very noticeable to humans are discarded. However, for scientific images discarding any image details may not be acceptable.

Still, all the images, except completely random ones, do include some redundancy. This permits lossless compression which does decrease image file size while preserving all the image details.

The simplest file compression can be achieved by using well-known arithmetic encoding of the image data. Arithmetic encoding compression degree can be calculated using Shannon entropy, which is just minus averaged base 2 Log of probabilities of all the values taken by the image pixels.

This Shannon entropy gives averaged number of bits per pixel which is necessary to arithmetically encode the image. If, say, the original image is a monochrome one with 8 bits per pixels, then for completely random image the entropy will be equal to 8. For non-random images the entropy will be less than 8.

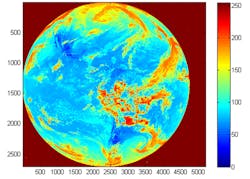
Let’s consider simple example of NASA infrared image of the Earth, shown here using false color

This image is 8-bit monochrome one, and has entropy of 5.85. This means arithmetic encoding can decrease image file size 1.367 times. This is better than nothing but not great.

Significant improvement can be achieved by transforming the image.

If we would use standard Lossless Wavelet compression (LWT), after one step of the LWT the initial image will be transformed into 4 smaller ones:

3 of these 4 smaller images contain only low pixel values which are not visible on the picture above.

Zooming on them saturates top left corner, but makes small details near other corners visible (notice the changed scale on the right):

Now the entropy of the top left corner 5.85, which is close to the entropy 5.87 of the complete initial image. The entropies of the other 3 corners are 1.83, 1.82 and 2.82. So, after only one LWT step the lossless compression ratio would be 2.6, which is significantly better than 1.367.

Our proprietary adaptive prediction lossless compression algorithm shows small prediction residue for the complete image:

Actual lossless compression ratio achieved here is about 4.06.

It is remarkable that while the last picture looks quite different from the original NASA image, it does contain all the information necessary to completely recover the initial image.

Due to lossless nature of the compression, the last picture, using arithmetic encoding, can be saved to the file 4.06 times smaller than the initial NASA picture file.

Our proprietary algorithm applied to this smaller file completely recovers the initial picture, accurately to the last bit. No bit left behind.

Learn More