OPTICAL FIBER MANUFACTURING: Stack-and-draw technique creates ultrasmall-diameter endoscopes
STEFAAN HEYVAERT, HEIDI OTTEVAERE, IRENEUSZ KUJAWA, RYSZARD BUCZYNSKI, and HUGO THIENPONT
The idea of using light and 'light guides' for an unobstructed, yet unobtrusive view of the human body's internal organs is not new. Phillip Bozzini, usually credited with the birth of modern endoscopy, successfully demonstrated what is considered to be the first endoscope in 1806. However, transmitting images from the distal end of the endoscope (inside the patient) to the proximal end (outside the patient) with sufficient resolution and field of view while limiting the outer diameter to a centimeter or less proved to be a technological challenge that was only resolved with the advent of fiber optics and the charge-coupled device (CCD) video chip.
Over the past few decades, advances in fiber optics and CCD technology have enabled large reductions in endoscope outer diameter, allowing the medical community to perform truly minimally invasive procedures. In addition, these technological advances have expanded diagnostic functionalities, giving rise to new types of endoscopy such as endomicroscopy.1
In fiber-optic endomicroscopy, the field of view (FOV) is sacrificed for a minimal outer diameter (<0.5 mm) to allow optical interrogation of tissue and organs that are not accessible with larger endoscopes. Since the minimal outer diameter does not allow for wide-field illumination and light collection, the tissue of interest needs to be raster-scanned by sequentially illuminating each point of the image plane. To achieve the beam steering necessary for raster scanning, two diametrically opposite approaches can be distinguished: the distal and the proximal approach.
In the distal approach, beam steering is accomplished using a micromechanical scanner-either a microelectromechanical systems (MEMS)-type device or a piezoelectric transducer (PZT) tube integrated in the distal tip of the endoscope.2,3 While this approach has shown some very promising results in terms of achievable resolution and FOV, its scalability remains to be proven since, to the best of our knowledge, the smallest diameter currently achieved is 1 mm.4
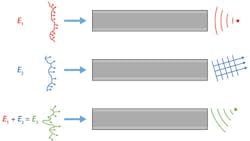
In the proximal approach, scanning and focusing of the light is achieved using appropriate spatial modulation of the light before it is coupled into the optical fiber (see Fig. 1). Because this method of proximal spatial light modulation (PSLM) does not require any additional microoptics or micromechanics at the distal end, it enables, in the opinion of the authors, the greatest potential for miniaturization.
In the past few years, endomicroscopy using PSLM has been explored by several groups desiring a fiber-optic endoscope with minimal footprint.5-7 In the last year, our team modeled, designed, and fabricated a coherent fiber bundle (CFB) to be used specifically with PSLM.8 This CFB consists of 550-nm-diameter, circular singlemode cores (Schott SF6 glass with refractive index n = 1.7817 at 850 nm) on a hexagonal lattice (lattice constant 1500 nm) in a common cladding material (NC21, a custom glass developed at ITME with n = 1.5211 at 850 nm) with a 0.098 numerical aperture.9
Stack-and-draw bundle fabrication
Fabrication of CFBs is performed at the Institute of Electronic Materials Technology (ITME) in Warsaw using the stack-and-draw technique. And while this technique is well-established for the fabrication of multicore and microstructured optical fibers, fabricating new designs requires a combination of science, craftsmanship, and trial and error.10 The latter is especially true for novel core-cladding material combinations (like in our CFB) since, depending on the desired value for the core-diameter-to-lattice-constant ratio, the differences in glass-softening temperature and expansion coefficients of core and cladding material (which can be quite considerable) must be taken into account and compensated for.11
The stack-and-draw technique essentially means stacking together rods of two different glasses into a macrostructure called a multirod preform and then, using a fiber drawing tower, slowly pulling this preform through a high-temperature furnace to scale it down in size (see Fig. 2).Design parameters of the CFB (such as core diameter and lattice constant) can be altered by varying the temperature (typically 600°-800°C for glasses and 150°–250°C for polymers) of the furnace as well as the seeding and pulling speed, defined as the speed with which the preform is fed through the furnace and the speed with which the bottom of the preform is pulled, respectively.12
Fabrication of the CFB begins with the manufacturing of several double-glass macro-rods, formed by taking a single glass rod with a high refractive index and diameter of a few tens of millimeters and placing it inside a glass tube with low refractive index (see Fig. 3). The ratio between the diameter of the internal macro-rod and the diameter of the total tube is chosen carefully as it will determine the dimensions and thus the optical characteristics of the final CFB.The final step of the process is a second drawing, whereby the macro-structured preform is pulled through the high-temperature furnace to scale it down to its final fiber size.
Realistic CFB performance modeling
Modeling and predicting our CFB's properties such as the light propagation characteristics or its point-spread function (PSF) require knowledge of its eigenmodes, which leads to a practical problem: for a CFB with a large number of singlemode cores (as is the case for our CFB that contains thousands of cores), determining all the eigenmodes for the complete structure leads to unwieldy computation times and memory demands.
Instead, we can use the spatial periodicity of the hexagonal lattice and define a 'unit cell' that can be seen as a spatial period of the complete CFB structure. By applying periodic boundary conditions in both the x and y directions, we can then calculate the unit cell's eigenmodes using Lumerical (Vancouver, BC, Canada) MODE solutions software—a fully vectorial mode solver based on a finite-difference engine.
Knowledge of the CFB's eigenmodes allows us to predict, for a given input field and length, the distal output field (or conversely, the necessary proximal input field for a desired distal output field). Determining the CFB's PSF is then a matter of propagating the distal output field towards the image plane using Rayleigh-Sommerfeld's diffraction integral.
For our model to be realistic, fabrication-induced deviations (that will always be present) should be taken into account, as they influence the CFB's eigenmodes. Scanning-electron microscopy (SEM) images of CFBs fabricated according to our design reveal that the most common types of deviations are variations in core size, core shape (ellipticity), and lattice constant.
To obtain quantitative data on these fabrication-induced deviations from the SEM images, we use Fiji, an open-source platform for image analysis.13 With Fiji, we first filter the images using a Gaussian convolution and convert them from 8-bit grayscale to black-and-white. In the next step, we use the 'Analyze Particles' function that automatically identifies the cores on the SEM image and extracts data such as core area, core shape (via fitting of an ellipse to each core), and position (coordinates of the core center with respect to the top left corner).
Cores that are only partially visible on the SEM images are excluded from the data set (see Fig. 5).8 Another advantage of the 'Analyze Particles' function is that dust particles, which are usually smaller and more irregular in shape than the cores, can also be excluded. The final output of the 'Analyze Particles' function is a table with statistics (average and standard deviation) on core size, core shape, and core position. Using these statistics, we can modify the aforementioned unit cell and recalculate the CFB's eigenmodes to account for the presence of each type of deviation (or a combination thereof).Outlook and future challenges
Currently, one of the challenges for PSLM-based endomicroscopy centers on the ability to both sense and compensate for changes in the geometry (such as bending) of the optical fiber. One approach recently proposed by researchers from EPFL in Switzerland uses a virtual, coherent beacon source holographically recorded on a photosensitive material covering the distal end of the optical fiber.14 The light back-reflected on the distal photosensitive material under illumination with the reference beam provides information on the fiber's geometry by comparing it with a look-up table containing the back-reflected light patterns for a set of known geometries. While this method allows focused beam delivery with a bent fiber, it does not allow imaging.
An alternative approach would be to integrate the optical fiber for PSLM with a three-core fiber-optic shape sensor into a common catheter, allowing for real-time knowledge of the catheter's shape.15 This could be combined with a CFB optimized for bending.
During the modeling process for our CFB, we found that if the cores were to be elliptical in shape and aligned along a common axis, the distal output would be linearly polarized (if the input polarization is correctly aligned to the common major or minor axis of the elliptical cores) as well as insensitive to all but the smallest (in terms of radius of curvature) of bending. In addition, the large difference in refractive index between core and cladding would ensure confinement, even for a high degree of bending.
REFERENCES
1. S. F. Elahi and T. D. Wang, J. Biophoton., 4, 7–8, 471–481 (2011).
2. H. C. Park et al., Opt. Lett., 37, 13, 2673–2675 (2012).
3. Y. Wu et al., Opt. Exp., 17, 10, 7907–7915 (2009).
4. C. M. Lee et al., J. Biophoton., 3, 5–6, 385–407 (2011).
5. T. Cizmar and K. Dholakia, Nat. Comm., 3, 1027 (2012); see http://bit.ly/1b5wNYu.
6. I. N. Papadopoulos et al., Opt. Exp., 20, 10, 10583–10590 (2012).
7. Y. Choi et al., Phys. Rev. Lett., 109, 20, 203901 (2012).
8. S. Heyvaert et al., Opt. Exp., 21, 19, 21991–22011 (2013).
9. D. Lorenc et al., Appl. Phys. B, 93, 2–3, 531–538 (2008).
10. R. Buczynski et al., Las. Phys., 22, 4, 784–790 (2012).
11. J. Nowosielski et al., Opt. Exp., 20, 11, 11767–11777 (2012).
12. A. Filipkowski et al., Opto-electron. Rev., 20, 3, 267–274 (2012).
13. J. Schindelin et al., Nat. Meth., 9, 7, 676–682 (2012).
14. S. Farahi et al., Opt. Exp., 21, 22504–22514 (2013).
15. J. P. Moore and M. D. Rogge, Opt. Exp., 20, 3, 2967–2973 (2012).
Stefaan Heyvaert is a PhD student, Heidi Ottevaere is a professor, and Hugo Thienpont is the department head of the Brussels Photonics Team (B-PHOT) of the Vrije Universiteit Brussel, Pleinlaan 2, 1050 Elsene, Building F - 9th floor, Brussels, Belgium; e-mail: [email protected]; www.b-phot.org. Ireneusz Kujawa is a research assistant and Ryszard Buczynski is a professor at the Institute of Electronics Materials Technology (ITME), 133 Wólczyńska Str., 01-919 Warsaw, Poland; http://www.itme.edu.pl/home-page.html.