Machine-vision software masters corner detection
Ben Dawson
In machine vision, edge-detection algorithms locate intensity transitions within an image that correspond to physical edges. Machine-vision systems use edges to locate, identify, and gauge parts. Corner-detection algorithms find junctions between two edges. Corners are better features than edges for some machine-vision applications. Corners fix a point on the part in two dimensions, are easier to uniquely identify, and have more information because they are less common.
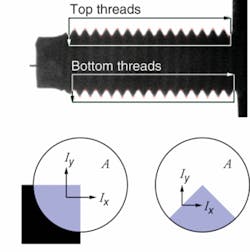
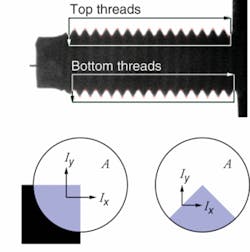
Sherlock machine-vision software from Dalsa IPD uses a Harris corner detector (described below) to locate corners, which can be used to count threads and measure distances between threads in a bolt (see figure, top). Corners are natural and fundamental features of this part, and these measurements would be difficult or impossible to make with single-edge detectors.
One way to think of edge detectors is that they find maximums of image-intensity derivatives, because edges have large contrast. For example, the Sobel edge detector uses two kernels.1 The I kernel takes the first derivative of image intensity in the x direction. Similarly, the I kernel takes the first derivative of image intensity in the y direction.
A corner has high-contrast edges that meet at a right angle. A corner detector might apply the Sobel edge detector in an image area, A, and sum the I and I intensity values. Large ΣI and ΣI values indicate strong edges in area A that could be a corner. This approach has two limitations. First, the Sobel output varies with edge angle, making it difficult to set an optimal detection threshold for various corner orientations (see figure, bottom). Second, we haven’t used the constraint that corner edges meet at a right angle to improve the detection sensitivity.
Harris corner detector
The Harris corner detector starts with the I and I derivative values from the Sobel (or another edge detector) in an image area A.2 A weighted Gaussian curve is applied to reduce the values further from the center of A.
In the standard exposition of the Harris corner detector, an autocorrelation matrix, C, is formed from these weighted values to model the results of small shifts in the corner position within area A. Another interpretation of this matrix is to think of C as a covariance matrix of the Gaussian-weighted derivatives around a zero mean. In this interpretation, we look for two axes of maximum variance of intensity derivatives. The magnitudes of the variance along these axes are the eigenvalues, λ1 and λ2, of matrix C. The eigenvalues make good measures for a corner detector because they are relatively constant under rotation and because edges meeting at a corner will have large values of λ1 and λ2. Lines will have only one large eigenvalue.
To visualize this, we plot weighted (I) values for each point in A. Corners generate two lines corresponding to the variation in the corner’s edge strength (due to the Gaussian weighting) and these lines intersect at the same angle as the corner’s lines. These lines rotate as the corner rotates, but their length variance stays nearly constant. Pick the line with the greatest length as an axis and measure variance along it and an orthogonal axis to enforce the right-angle corner contraint. Both variances, equivalent to λ1 and λ2, will be large only when we have a right-angle corner.
Corners are detected by applying the following three rules to λ1 and λ2. If both values are small, area A has no edge or corner. When one value is large and the other small, then A has an edge or a corner that is much larger or smaller than a right angle. If both values are large, A has a right-angle corner.
Other corner detectors are based on derivatives or on integration (counting). For example, the Smallest Univalue Segment Assimilating Nucleus (SUSAN) edge and corner detector counts the number of pixels that have intensity similar to a center pixel in an image window.3 When this count is small, you have an edge, and when it is even smaller, a corner. Lines and spots of noise will have the smallest count, so noise is effectively suppressed and corners are detected correctly.
Corner detection at work
There are some practical considerations when using corner detection. In general, the larger the corner contrast and the closer the corner is to a right angle, the stronger the indicated “corner strength.” Corner detection is often not practical on highly textured or noisy images. For example, spots of noise or lines protruding from a part are often marked as corners by a corner detector. In some cases, a median filter can remove spot noise, but be careful-the median filter can take a “bite” out of corners. Protruding lines usually trigger small corner detection strengths because only one dimension of the differential operator is activated.
One practical feature of the Sherlock machine-vision software is that it can suppress corner detection within some radius of a found corner. This is helpful when detecting corners in a periodic structure, such as a bolt, as it reduces the chance of false corner detection, perhaps caused by noise.
As part of the Sherlock software, the Harris corner detector has a position accuracy of about one pixel, which is often not enough. Sherlock provides two methods for improving the accuracy of the corner location, one based on the corner centroid and another on search. The latter method has about 1/5-pixel accuracy.
For parts that naturally have corners and are low in texture and noise, a corner detector is the tool of choice. Examples of parts where corner detection works well include bolts, gears, printed-circuit-board pads, boxes, electrical connectors, cutting tools, stamped metal parts, and screen or grid patterns. Once you’ve experienced the power of corner detection, you will find many applications for which it is the best choice.
REFERENCES
1. W.K. Pratt, Digital Image Processing, John Wiley & Sons, NY (487) 1978.
2. C. Harris and M. Stephens, Proc. Alvey Vision Conf., Manchester, England (1988).
3. users.fmrib.ox.ac.uk/~steve/susan/susan/susan.html
Tell us what you think about this article. Send an e-mail to [email protected].
BEN DAWSON is director of Strategic Development at DALSA IPD, 700 Technology Park Dr., Billerica, MA 01821; e-mail: [email protected]; www.dalsa.com.