Wavelet-based image processing enhances mammography
Wavelet-based image processing enhances mammography
Andrew F. Laine
Mammography is widely recognized as the only effective imaging technique for the early detection of breast cancer. Early detection is a key ingredient of any
strategy designed to reduce breast cancer mortality.
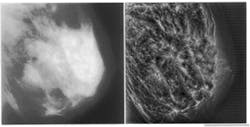
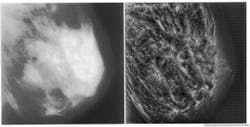
Detection of early malignancies while they are still small is problematical, especially in younger women who have denser breast tissue, because of the minor difference in x-ray attenuation between normal glandular tissues and malignant disease (see Fig. 1, left). Although calcifications present with malignancy may have high inherent attenuation properties, their small size also results in a low subject contrast. As a result, tumor detection will always be difficult in mammography done with analog film or screen imaging. Because mammograms display only about 3% of the information they detect, improvements in detection of small tumors and microcalcifications are more likely to occur by improving the visibility of these features.
Both multiorientation and multiresolution are known features of the human visual system?certain cortical neurons respond specifically to stimuli within certain orientations and frequencies. Using multiscale image-processing algorithms, we can exploit the orientation and frequency selectivity of wavelet transforms to make mammographic features more obvious to human observation through localized contrast gain.
A wavelet transform is a decomposition of an image into a family of functions. A windowed Fourier transform has a fixed resolution in the spatial and frequency domains. In comparison, the resolution of a wavelet transform varies with a scale parameter, decomposing an image into a set of frequency channels of constant bandwidth on a logarithmic scale. This variation of resolution enables a wavelet transform to OzoomO into the irregularities of an image and to characterize them locally.
Framework for multiscale analysis
With mammographic feature analysis via multiresolution representations, highly detailed image reconstruction is possible. Multiscale wavelet representations suggest a mathematically coherent basis not only for using existing multigrid techniques, but also for exploiting nonlinear systems. Multiresolution wavelet analysis provides a natural hierarchy that can contain pattern-analysis protocols for accomplishing feature analysis in scale-space, which is an imaging hierarchy of multiple scales. As with traditional coarse-to-fine matching strategies, the radiologist may first choose to look for coarse features, such as dominant masses, within low-frequency levels of the wavelet transform. Finer features, such as microcalcifications, can then be examined at higher frequency levels (see Fig. 1, right).
Choosing wavelets, or analyzing functions, that are simultaneously localized in both space and frequency results in a powerful methodology for analyzing a mammogram. The inner product of an information signal, f with a wavelet y is {f, y } = (2?)?1{foyo} and reflects the character of f within the time-frequency region where y is localized. The fo andyo are Fourier transforms of the analyzing function and the signal, respectively. If y is spatially localized, then two-dimensional features such as shape and orientation are preserved in the transform space and may characterize a feature through scale-space. We may OextractO? such features by applying geometric constraints for edge detection within each level of the transform.
For the dense tissue images, the values of transform coefficients within each level of a two-channel wavelet filter bank, consisting of horizontal and vertical subbanks, were independently modified by histogram equalization. The histogram represents the frequency of occurrence of a particular wavelet coefficient value. Because the coefficients are space-frequency representations, contrast modifications on the transform side are preserved in part on the spatial side after reconstruction.
The complexity of a reconstructed mammogram can be reduced by selecting a subset of features that satisfy certain geometric constraints. An illustration would be choosing to focus on only those features oriented in a particular direction. Subsequent image reconstructions can then use the context provided by previously enhanced features to investigate additional characteristics that emerge at other scales and orientations (see Fig. 2). For example, fine vertical features can be selected and analyzed in the context of previously classified large horizontal features. Thus, the strategy provides a global context in which subtle features within finer scales might be classified incrementally through a precomputed hierarchy of scale-space.
Experimental results
In general, improvements in image contrast achieved with multiscale image processing algorithms were superior to those obtained using competitive algorithms of unsharp masking and adaptive histogram equalization. Preliminary results have shown that wavelet-transform-based multiscale processing techniques can make hard-to-discern attributes of a mammogram more obvious without requiring additional patient radiation exposure. These analyzing functions can improve the visualization of features important to mammography and assist radiologists in the early detection of breast cancer.
But although the results are very encouraging, further studies are needed to identify the most promising approaches of multiscale-based image-processing algorithms. Ultimately, however, the objective of any image processing is to improve the visibility of clinically significant features in mammograms. Accordingly, the most promising algorithms require evaluation using clinical mammograms. Such tests will be designed to measure the ability of multiscale image processing to significantly improve the sensitivity, specificity, and overall accuracy of mammographic interpretation. n
FIGURE 1. Lack of contrast makes dense-tissue mammograms particularly difficult to diagnose (left); image gains in contrast after global wavelet processing for four levels of analysis (right).
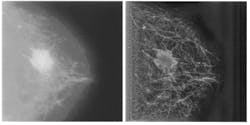
FIGURE 2. Subtle structural features around a spicular mass are not visible in unprocessed mammogram (left). Multiscale processing using a nonseparable, nonorthogonal analyzing function reveals
calcifications and penetration of fibroglandular structures into the obvious mass tissue (right). The geometric shapes of the calcifications are seen more clearly, as are the ductules and arterial structures.