Imaging Theory: Breaking Rayleigh's limit: Imaging resolution not defined by the criterion

The limits of optical resolution for an imaging system have long been defined by the Rayleigh criterion: imaging points can only be resolved if they are separated by half the spot size of the diffraction-limited point spread function (PSF) of the imaging system (with half the spot size being defined as the distance from the central maximum to the first minimum). Essentially, diffraction is the fundamental hurdle to increasing imaging resolution, smearing out the spatial distribution of light that reaches an imaging detector.

There are ways to subvert the Rayleigh criterion, including the use of near-field optics, which capture evanescent as well as free-space electromagnetic waves and the capture of Rabi oscillations. Unfortunately, these approaches are complex and often not useful in practical optical systems.

By revisiting the quantum nature of light, however, researchers at Palacký University (Olomouc, Czech Republic) and Universidad Complutense (Madrid, Spain) have found a more straightforward way to determine the achievable resolution limit of an imaging system that does not depend on diffraction effects.¹

Quantum metrology

Using quantum Fisher information (QFI)—a mathematical measure of the sensitivity of an observable quantity (in this case the PSF) to changes in its underlying parameters (emitter positions and intensities), the separation between two poorly resolved and incoherent point sources is estimated and bound by the quantum Cramér-Rao lower bound (qCRLB). In more physical terms, the Rayleigh criterion is based on intensity scans, which discard all phase information. When the proper strategy is chosen, and complete information is gathered, the Rayleigh limit turns out to be nonessential. By studying circular and slit apertures, the QFI and qCRLB criteria can be implemented in a compact optical setup to analyze the resolvable separation of two points at distances below the Rayleigh limit.

Assuming quasimonochromatic paraxial waves with one specified polarization and one spatial dimension, a quantum parlance is used to characterize the PSF of two incoherent point sources entering an imaging system. A sensible estimate of the separation of those point sources requires the establishment of a measurement strategy that encompasses the complete information carried by the field.

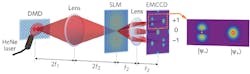
To separate the spatial modes in the image plane, a digital micromirror controls the emitter points until the images coalesce (see figure). Separations 17X smaller than the Rayleigh limit were observed for the Gaussian aperture and 10X smaller for the slit aperture.

In summary, the simple technique used here improves over traditional means of imaging theory in resolving two closely spaced point sources. No special sources or equipment are needed to complete the setup, and results demonstrate that diffraction limits are not a fundamental constraint to imaging resolution.

Researcher Luis L. Sanchez-Soto of Universidad Complutense says, "The optics textbooks have to be revised. It is not that the Rayleigh criterion is wrong, it is just that it applies only for a particular detection scheme—the intensity scan—that is not very efficient in conveying the information carried by the optical field."

REFERENCE

1. M. Paúr et al., Optica, 3, 10, 1144–1147 (2016).